题目内容
【题目】已知圆 ![]() 的圆心在直线
的圆心在直线 ![]() 上,且圆
上,且圆 ![]() 经过点
经过点 ![]() .
.
(1)求圆的标准方程;
(2)直线 ![]() 过点
过点 ![]() 且与圆
且与圆 ![]() 相交,所得弦长为4,求直线
相交,所得弦长为4,求直线 ![]() 的方程.
的方程.
【答案】
(1)解:设圆心为 ![]() ,则
,则 ![]() 应在
应在 ![]() 的中垂线上,其方程为
的中垂线上,其方程为 ![]() ,
,
由 ![]() ,即圆心
,即圆心 ![]() 坐标为
坐标为 ![]()
又半径 ![]() ,故圆的方程为
,故圆的方程为 ![]()
(2)解:点 ![]() 在圆内,且弦长为
在圆内,且弦长为 ![]() ,故应有两条直线.
,故应有两条直线.
圆心到直线距离 ![]() .
.
①当直线的斜率不存在时,直线的方程为 ![]() ,
,
此时圆心到直线距离为1,符合题意.
②当直线的斜率存在时,设为 ![]() ,直线方程为
,直线方程为 ![]()
整理为 ![]() ,则圆心到直线距离为
,则圆心到直线距离为 ![]()
解得 ![]() ,直线方程为
,直线方程为 ![]()
综上①②,所求直线方程为 ![]() 或
或 ![]()
【解析】(1)圆心为 两条弦所在直线相交点,利用方程组求出圆心,两点距离求出半径,得到圆的标准方程 。
(2)讨论斜率存在与否 ,设出直线方程, 利用垂径定理求出圆心到直线的距离,由点到直线距离公式求出斜率K,得到直线方程。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】某校为调查高一、高二学生周日在家学习用时情况,随机抽取了高一、高二各![]() 人,对他们的学习时间进行了统计,分别得到了高一学生学习时间(单位:小时)的频数分布表和高二学生学习时间的频率分布直方图.
人,对他们的学习时间进行了统计,分别得到了高一学生学习时间(单位:小时)的频数分布表和高二学生学习时间的频率分布直方图.
高一学生学习时间的频数分布表(学习时间均在区间![]() 内):
内):
学习时间 |
|
|
|
|
|
|
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
高二学生学习时间的频率分布直方图:
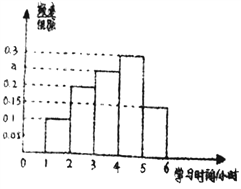
(1)求高二学生学习时间的频率分布直方图中的![]() 值,并根据此频率分布直方图估计该校高二学生学习时间的中位数;
值,并根据此频率分布直方图估计该校高二学生学习时间的中位数;
(2)利用分层抽样的方法,从高一学生学习时间在![]() ,
,![]() 的两组里随机抽取
的两组里随机抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,求学习时间在
人,求学习时间在![]() 这一组中至少有
这一组中至少有![]() 人被抽中的概率.
人被抽中的概率.
