题目内容
【题目】已知点 
为坐标原点， 
是椭圆 
上的两个动点，满足直线 
与直线 
关于直线 
对称.
（1）证明直线 
的斜率为定值，并求出这个定值；
（2）求 
的面积最大时直线 的方程.
【答案】
（1）证明：设直线 
方程为： 
，代入 
得
设 
，因为点 
在椭圆上，所以
又由题知，直线 
的斜率与 的斜率互为相反数，在上式中以 
代 
，可得
，
所以直线 
的斜率 
故答案为:直线 的斜率为定值，其值为 
（2）解：由（1）可设直线 方程为： 
，代入 得
，则 
.由 
可得 
.
， 
到直线 的距离 
，
可得 
，
当且仅当 
（满足 ），即 
时取等.
故答案为:直线 的方程为： 
，或 
.
【解析】(1)将直线方程代入椭圆方程中消去y得关于x的一元二次方程,由韦达定理得到两根和与积,由斜率公式求斜率;
(2)将三角形的面积表示为m的函数式,由二次函数求最值.
练习册系列答案
相关题目
【题目】某校为调查高一、高二学生周日在家学习用时情况，随机抽取了高一、高二各
人，对他们的学习时间进行了统计，分别得到了高一学生学习时间（单位：小时）的频数分布表和高二学生学习时间的频率分布直方图.
高一学生学习时间的频数分布表（学习时间均在区间
内）：
学习时间 |
|
|
|
|
|
|
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
高二学生学习时间的频率分布直方图：
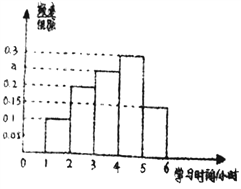
（1）求高二学生学习时间的频率分布直方图中的
值，并根据此频率分布直方图估计该校高二学生学习时间的中位数；
（2）利用分层抽样的方法，从高一学生学习时间在
，
的两组里随机抽取
人，再从这人中随机抽取
人，求学习时间在这一组中至少有
人被抽中的概率.
