题目内容
【题目】已知函数f(x)= ![]() sinωx﹣
sinωx﹣ ![]() cosωx(ω<0),若y=f(x+
cosωx(ω<0),若y=f(x+ ![]() )的图象与y=f(x﹣
)的图象与y=f(x﹣ ![]() )的图象重合,记ω的最大值为ω0 , 函数g(x)=cos(ω0x﹣
)的图象重合,记ω的最大值为ω0 , 函数g(x)=cos(ω0x﹣ ![]() )的单调递增区间为( )
)的单调递增区间为( )
A.[﹣ ![]() π+
π+ ![]() ,﹣
,﹣ ![]() +
+ ![]() ](k∈Z)
](k∈Z)
B.[﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() ](k∈Z)
](k∈Z)
C.[﹣ ![]() π+2kπ,﹣
π+2kπ,﹣ ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
D.[﹣ ![]() +2kπ,﹣
+2kπ,﹣ ![]() +2kπ](k∈Z)
+2kπ](k∈Z)
【答案】A
【解析】解:函数f(x)= ![]() sinωx﹣
sinωx﹣ ![]() cosωx(ω<0)=2sin(ωx﹣
cosωx(ω<0)=2sin(ωx﹣ ![]() ), 若y=f(x+
), 若y=f(x+ ![]() )的图象与y=f(x﹣
)的图象与y=f(x﹣ ![]() )的图象重合,
)的图象重合,
则 ![]() 为函数f(x)的周期,即
为函数f(x)的周期,即 ![]() =k|
=k| ![]() |,∴ω=±4k,k∈Z.
|,∴ω=±4k,k∈Z.
记ω的最大值为ω0 , 则ω0=﹣4,
函数g(x)=cos(ω0x﹣ ![]() )=cos(﹣4x﹣
)=cos(﹣4x﹣ ![]() )=cos(4k+
)=cos(4k+ ![]() ).
).
令2kπ﹣π≤4x+ ![]() ≤2kπ,求得
≤2kπ,求得 ![]() ﹣
﹣ ![]() ≤x≤
≤x≤ ![]() ﹣
﹣ ![]() ,
,
故函数g(x)的增区间为[ ![]() ﹣
﹣ ![]() ,
, ![]() ﹣
﹣ ![]() ],k∈Z.
],k∈Z.
故选:A.
利用三角恒等变换化简f(x)的解析式,利用正弦函数的周期性求得ω的值,再利用余弦函数的单调性,求得函数g(x)的增区间.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表.
组号 | 分组 | 频率 |
第1组 | [160,165) | 0.05 |
第2组 |
| 0.35 |
第3组 |
| 0.3 |
第4组 |
| 0.2 |
第5组 |
| 0.1 |
合计 | 1.00 | |
(Ⅰ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样的方法抽取6名学生进行体能测试,问第3,4,5组每组各应抽取多少名学生进行测试;
(Ⅱ)在(Ⅰ)的前提下,学校决定在6名学生中随机抽取2名学生进行引体向上测试,求第3组中至少有一名学生被抽中的概率;
(Ⅲ)试估计该中学高三年级男生身高的中位数位于第几组中,并说明理由.
【题目】某校为调查高一、高二学生周日在家学习用时情况,随机抽取了高一、高二各![]() 人,对他们的学习时间进行了统计,分别得到了高一学生学习时间(单位:小时)的频数分布表和高二学生学习时间的频率分布直方图.
人,对他们的学习时间进行了统计,分别得到了高一学生学习时间(单位:小时)的频数分布表和高二学生学习时间的频率分布直方图.
高一学生学习时间的频数分布表(学习时间均在区间![]() 内):
内):
学习时间 |
|
|
|
|
|
|
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
高二学生学习时间的频率分布直方图:
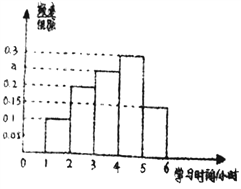
(1)求高二学生学习时间的频率分布直方图中的![]() 值,并根据此频率分布直方图估计该校高二学生学习时间的中位数;
值,并根据此频率分布直方图估计该校高二学生学习时间的中位数;
(2)利用分层抽样的方法,从高一学生学习时间在![]() ,
,![]() 的两组里随机抽取
的两组里随机抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,求学习时间在
人,求学习时间在![]() 这一组中至少有
这一组中至少有![]() 人被抽中的概率.
人被抽中的概率.