题目内容
【题目】已知各项均为正数的数列{an}的前n项和为Sn ， 且Sn满足n（n+1）Sn2+（n2+n﹣1）Sn﹣1=0（n∈N*），则S1+S2+…+S2017= ．
【答案】
【解析】解：∵n（n+1）Sn2+（n2+n﹣1）Sn﹣1=0（n∈N*）， ∴[n（n+1）Sn﹣1]（Sn+1）=0，Sn＞0．
∴n（n+1）Sn﹣1=0，
∴Sn= 
= 
﹣ 
．
∴S1+S2+…+S2017= 
+…+ 
= ．
所以答案是： ．
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系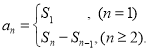
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
【题目】某中学从高三男生中随机抽取100名学生，将他们的身高数据进行整理，得到下侧的频率分布表.
组号 | 分组 | 频率 |
第1组 | [160，165） | 0.05 |
第2组 |
| 0.35 |
第3组 |
| 0.3 |
第4组 |
| 0.2 |
第5组 |
| 0.1 |
合计 | 1.00 | |
（Ⅰ）为了能对学生的体能做进一步了解，该校决定在第3，4，5组中用分层抽样的方法抽取6名学生进行体能测试，问第3，4，5组每组各应抽取多少名学生进行测试；
（Ⅱ）在（Ⅰ）的前提下，学校决定在6名学生中随机抽取2名学生进行引体向上测试，求第3组中至少有一名学生被抽中的概率；
（Ⅲ）试估计该中学高三年级男生身高的中位数位于第几组中，并说明理由.
【题目】某校为调查高一、高二学生周日在家学习用时情况，随机抽取了高一、高二各
人，对他们的学习时间进行了统计，分别得到了高一学生学习时间（单位：小时）的频数分布表和高二学生学习时间的频率分布直方图.
高一学生学习时间的频数分布表（学习时间均在区间
内）：
学习时间 |
|
|
|
|
|
|
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
高二学生学习时间的频率分布直方图：
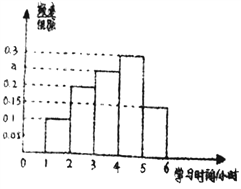
（1）求高二学生学习时间的频率分布直方图中的
值，并根据此频率分布直方图估计该校高二学生学习时间的中位数；
（2）利用分层抽样的方法，从高一学生学习时间在
，
的两组里随机抽取
人，再从这人中随机抽取
人，求学习时间在这一组中至少有
人被抽中的概率.
