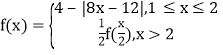题目内容
【题目】已知在平面直角坐标系xOy中，椭圆C：
（a＞b＞0）离心率为
，其短轴长为2．
（1）求椭圆C的标准方程；
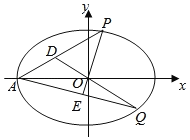
（2）如图，A为椭圆C的左顶点，P，Q为椭圆C上两动点，直线PO交AQ于E，直线QO交AP于D，直线OP与直线OQ的斜率分别为k1，k2，且k1k2＝
，
（λ，μ为非零实数），求λ2+μ2的值．
【答案】（1）
；（2）1
【解析】
（1）由题意可得b＝1，运用离心率公式和a，b，c的关系，可得a，b，进而得到椭圆方程；
（2）求得A的坐标，设P（x1，y1），D（x0，y0），运用向量共线坐标表示，结合条件求得P的坐标，代入椭圆方程，可得λ2＝
，同理得μ2＝
，即可得λ2+μ2的值．
（1）因为短轴长2b＝2，所以b＝1，又离心率e＝
，且a2﹣b2＝c2，
解得a＝
，c＝1，则椭圆C的方程为
+y2＝1；
（2）由（1）可得点 A（﹣，0），设P（x1，y1），D（x0，y0），则y1＝k1x1，y0＝k2x0，
由
可得x0+＝λ（x
﹣x0），y0＝λ（y1﹣y0），
即有x0＝
，k1x1＝y1＝
y0＝k2x0＝k2（x1﹣
），
两边同乘以k1，可得k12x1＝k1k2（x1﹣）＝﹣
（x1﹣），
解得x1＝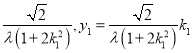
，将P（x1，y1）代入椭圆方程可得λ2＝，
由
可得μ2＝
，可得λ2+μ2＝1．
练习册系列答案
相关题目
