题目内容
【题目】已知点P(t,t![]() 1),t∈R,点E是圆
1),t∈R,点E是圆![]() 上的动点,点F是圆
上的动点,点F是圆![]() 上的动点,则|PF|
上的动点,则|PF|![]() |PE|的最大值为______
|PE|的最大值为______
【答案】4
【解析】
结合图象发现两圆位于P点所在直线的不同侧,应先作出圆O:![]() 关于直线y=x
关于直线y=x![]() 1对称的圆O1,把|PF|
1对称的圆O1,把|PF|![]() |PE|转化为|PF|
|PE|转化为|PF|![]() |PE′|,要使|PF|
|PE′|,要使|PF|![]() |PE′|最大,则必须|PF|最大,|PE′|最小.
|PE′|最大,则必须|PF|最大,|PE′|最小.
∵P(t,t![]() 1)∴P点在直线y=x
1)∴P点在直线y=x![]() 1上,
1上,
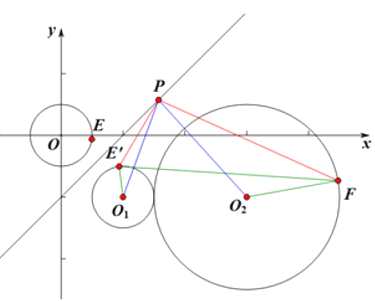
作E关于直线y=x![]() 1的对称点E′,且圆O:
1的对称点E′,且圆O:![]() 关于直线y=x
关于直线y=x![]() 1对称的圆O1方程为:(x
1对称的圆O1方程为:(x![]() 1)2+(y+1)2=
1)2+(y+1)2=![]() ,
,
所以E′在圆O1上,∴|PE|=|PE′|,
设圆![]() 的圆心为O2,
的圆心为O2,
∴|PE′|≥|PO1|![]() |E′O1|,|PF|≤|PO2|+|FO2|,
|E′O1|,|PF|≤|PO2|+|FO2|,
∴|PF|![]() |PE|=|PF|
|PE|=|PF|![]() |PE′|≤(|PO2|+|FO2|)
|PE′|≤(|PO2|+|FO2|)![]() (|PO1|
(|PO1|![]() |E′O1|)=|PO2|
|E′O1|)=|PO2|![]() |PO1|+2≤|O1O2|+2=4,
|PO1|+2≤|O1O2|+2=4,
当P、E′、F、O1、O2五点共线,E′在线段PO1上,O2在线段PF上时成立.
因此,|PF|![]() |PE|的最大值为4.
|PE|的最大值为4.
故答案为4.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
【题目】越接近高考学生焦虑程度越强,四个高三学生中大约有一个有焦虑症,经有关机构调查,得出距离高考周数与焦虑程度对应的正常值变化情况如下表周数
周数x | 6 | 5 | 4 | 3 | 2 | 1. |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
其中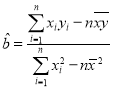 ,
,![]() ,
,![]() ,
,![]()
(1)作出散点图;
(2)根据上表数据用最小二乘法求出y关于x的线性回方程![]() (精确到0.01)
(精确到0.01)
(3)根据经验观测值为正常值的0.85~1.06为正常,若1.06~1.12为轻度焦虑,1.12~1.20为中度焦虑,1.20及以上为重度焦虑。若为中度焦虑及以上,则要进行心理疏导。若一个学生在距高考第二周时观测值为103,则该学生是否需要进行心理疏导?