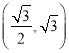题目内容
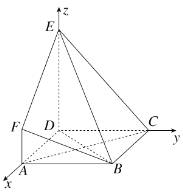
【题目】如下图所示,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°.

(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
【答案】(1)见解析 (2)![]() (3)M的坐标为(2,2,0),见解析
(3)M的坐标为(2,2,0),见解析
【解析】解:(1)∵DE⊥平面ABCD,∴DE⊥AC,∵ABCD是正方形,∴AC⊥BD,又DE∩BD=D,∴AC⊥平面BDE.
(2)∵DE⊥平面ABCD,∴∠EBD就是BE与平面ABCD所成的角,即∠EBD=60°.
∴![]() =
=![]() .由AD=3,得DE=3
.由AD=3,得DE=3![]() ,AF=
,AF=![]() .
.
如图所示,分别以DA,DC,DE所在直线为x轴、y轴、z轴建立空间直角坐标系,则A(3,0,0),F(3,0,![]() ),E(0,0,3
),E(0,0,3![]() ),B(3,3,0),C(0,3,0),
),B(3,3,0),C(0,3,0),
∴![]() =(0,-3,
=(0,-3,![]() ),
),![]() =(3,0,-2
=(3,0,-2![]() ).
).
设平面BEF的法向量为n=(x,y,z),则
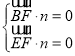 ,即
,即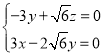 .
.
令z=![]() ,则n=(4,2,
,则n=(4,2,![]() ).
).
∵AC⊥平面BDE,
∴![]() =(3,-3,0)为平面BDE的一个法向量,
=(3,-3,0)为平面BDE的一个法向量,
∴cos〈n,![]() 〉=
〉=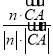 =
=![]() =
=![]() .
.
又二面角F-BE-D为锐角,故二面角F-BE-D的余弦值为![]() .
.
(3)依题意,设M(t,t,0)(0≤t≤3),则![]() =(t-3,t,0),
=(t-3,t,0),
∴AM∥平面BEF,∴![]() ·n=0,
·n=0,
即4(t-3)+2t=0,解得t=2.
∴点M的坐标为(2,2,0),此时![]() =
=![]()
![]() ,
,
∴点M是线段BD上靠近B点的三等分点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目