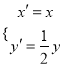题目内容
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)若a=1,求曲线f(x)在点(e,f(e))处的切线方程;
(Ⅱ)求f(x)的极值;
(Ⅲ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围.
【答案】(1) x+e2y-3e=0 (2) a≥1.
【解析】试题分析:(Ⅰ)由切点坐标,根据导数的几何意义,求出该点的导数值,即得曲线在此点处的切线的斜率,然后用点斜式写出切线方程即可;(Ⅱ)求出函数![]() 的导函数,令导数大于0解出增区间,令导数小于0,解出函数的减区间,然后由极值判断规则确定出极值即可;
的导函数,令导数大于0解出增区间,令导数小于0,解出函数的减区间,然后由极值判断规则确定出极值即可;
(Ⅲ)若函数![]() 的图象与函数
的图象与函数![]() 的图象在区间
的图象在区间![]() 上有公共点,即在区间
上有公共点,即在区间![]() 上,函数
上,函数![]() 存在自变量取某个值时,函数值等于1,故问题可以转化为求出函数
存在自变量取某个值时,函数值等于1,故问题可以转化为求出函数![]() 最值,保证函数的最大值大于等于1,最小值小于等于1,即可得到关于参数
最值,保证函数的最大值大于等于1,最小值小于等于1,即可得到关于参数![]() 的不等式,解之即得.
的不等式,解之即得.
试题解析:(Ⅰ) a=1, ![]() 且
且![]()
又∵![]()
∴![]()
∴f(x)在点(e,f(e))处的切线方程为: ![]() ,即x+e2y-3e=0.
,即x+e2y-3e=0.
(Ⅱ)f(x)的定义域为(0,+∞), ![]()
令f′(x)=0得x=e1-a.
当x∈(0,e1-a)时,f′(x)>0,f(x)是增函数;
当x∈(e1-a,+∞)时,f′(x)<0,f(x)是减函数;
f(x)在x=e1-a处取得极大值,
即f(x)极大值=f(e1-a)=ea-1
(Ⅲ)(i)当e1-a<e2,即a>-1时,
由(Ⅱ)知f(x)在(0,e1-a)上是增函数,
在(e1-a,e2]上是减函数,
当x=e1-a时,f(x)取得最大值,
即f(x)max=ea-1.
又当x=e-a时,f(x)=0,
当x∈(0,e-a]时,f(x)<0,
当x∈(e-a,e2]时,f(x)∈(0,ea-1],
所以,f(x)的图象与g(x)=1的图象在(0,e2]上有公共点,
等价于ea-1≥1,解得a≥1,
又因为a>-1,所以a≥1.
(ii)当e1-a≥e2,即a≤-1时,f(x)在(0,e2]上是增函数,
f(x)在(0,e2]上的最大值为f(e2)=![]() ,
,
原问题等价于![]() ≥1,解得a≥e2-2,
≥1,解得a≥e2-2,
又a≤-1 无解
综上,a的取值范围是a≥1.