题目内容
20.已知⊙C的极坐标方程为:ρ2-4$\sqrt{2}ρsin(θ+\frac{π}{4})+6=0$(Ⅰ)求圆C在直角坐标系中的圆心坐标,并选择合适的参数,写出圆C的参数方程;
(Ⅱ)点P(x,y)在圆C上,试求u=xy的值域.
分析 取极点为直角坐标系中的原点,极轴为直角坐标系中的x轴,:ρ2-4$\sqrt{2}ρsin(θ+\frac{π}{4})+6=0$展开化为ρ2-4ρsinθ-4ρcosθ+6=0,利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可化为直角坐标方程.再利用圆的参数方程与三角函数的单调性即可得出.
解答 解:取极点为直角坐标系中的原点,极轴为直角坐标系中的x轴,:ρ2-4$\sqrt{2}ρsin(θ+\frac{π}{4})+6=0$展开化为ρ2-4ρsinθ-4ρcosθ+6=0,可得:x2+y2-4x-4y+6=0,∴(x-2)2+(y-2)2=2,圆C的圆心坐标为(2,2),半径为$\sqrt{2}$,
(2)取旋转角α为参数,则圆C的参数方程为C:$\left\{\begin{array}{l}x=2+\sqrt{2}cosα\\ y=2+\sqrt{2}sinα\end{array}\right.(α为参变数)$,
∵$u=x•y=(2+\sqrt{2}cosα)(2+\sqrt{2}sinα)=4+2\sqrt{2}(sinα+cosα)+2sinαcosα$,
设$t=sinα+cosα=\sqrt{2}sin(α+\frac{π}{4})⇒\left\{\begin{array}{l}2sinαcosα={t^2}-1\\-\sqrt{2}≤t≤\sqrt{2}\end{array}\right.$,
∴u=f(t)=$2\sqrt{2}t+{t}^{2}$-1+4=$(t+\sqrt{2})^{2}$+1$(-\sqrt{2}≤t≤\sqrt{2})$.
∴1≤u≤9.
∴u的值域为[1,9].
点评 本题考查了参数方程的应用、极坐标化为直角坐标方程、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

| A. | x2+y2-8x=0 | B. | y=6x2 | C. | x2+4y2=1 | D. | $\frac{x^2}{9}-\frac{y^2}{4}$=1 |
| A. | $f(0)<f(\frac{3}{5})<f(-\frac{1}{2})$ | B. | $f(0)<f(-\frac{1}{2})<f(\frac{3}{5})$ | C. | $f(\frac{3}{5})<f(-\frac{1}{2})<f(0)$ | D. | $f(-\frac{1}{2})<f(0)<f(\frac{3}{5})$ |
| A. | $\frac{2}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{π}{4}$ | D. | $\frac{1}{2π}$ |
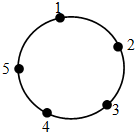 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.