题目内容
16.已知函数$f(x)=\left\{\begin{array}{l}-{x^2}\;,\;x≥0\\{x^2}+2x,\;x<0\end{array}\right.$,则f(2)=-4;不等式f(x)<3的解{x|x>-3}.分析 (1)将x=2代入函数的表达式,求出f(2)即可;
(2)分别解-x2<3,x2+2x<3,从而求出不等式的解.
解答 解:(1)x≥0时,
f(x)=-x2,
∴f(2)=-4;
(2)①x≥0时,-x2<3,∴x≥0,
②x<0时,x2+2x<3,解得:-3<x<0,
综合①②得:x>-3,
故答案为:-4,{x|x>-3}.
点评 本题考察了分段函数的应用,考察不等式的解法问题,是一道基础题.

练习册系列答案
相关题目
1.已知数列{an}的通项公式为${a_n}={2^{5-n}}$,数列{bn}的通项公式为bn=n+k,设${c_n}=\left\{\begin{array}{l}{b_n},{a_n}≤{b_n}\\{a_n},{a_n}>{b_n}\end{array}\right.$,若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是( )
| A. | -5≤k≤-4 | B. | -4≤k≤-3 | C. | -5≤k≤-3 | D. | k=-4 |
5.已知函数f(x)=x2-cosx,则$f(\frac{3}{5}),f(0),f(-\frac{1}{2})$的大小关系是( )
| A. | $f(0)<f(\frac{3}{5})<f(-\frac{1}{2})$ | B. | $f(0)<f(-\frac{1}{2})<f(\frac{3}{5})$ | C. | $f(\frac{3}{5})<f(-\frac{1}{2})<f(0)$ | D. | $f(-\frac{1}{2})<f(0)<f(\frac{3}{5})$ |
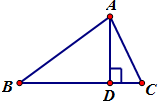 如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )
如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )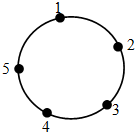 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.