题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}-{x^2}\;,\;x≥0\\{x^2}+2x,\;x<0\end{array}$,则f(f(-2))=0;不等式f(f(x))≤3的解集为(-∞,$\sqrt{3}$].分析 根据分段函数的表达式进行求解即可.
解答 解:由分段函数得f(-2)=4-4=0,则f(f(-2))=f(0)=-0=0,
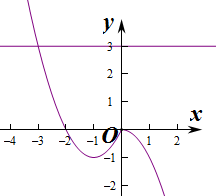 设t=f(x),
设t=f(x),
则不等式f(f(x))≤3等价为f(t)≤3,
由图象知t≥-3,
即f(x)≥-3,
若x≥0,由-x2≥-3得x2≤3,解得0≤x≤$\sqrt{3}$,
若x<0,2x+x2≥3,得x2+2x-3≥0,
解得x≥1或x≤-3,此时x<0,
综上x≤$\sqrt{3}$,
即不等式的解集为(-∞,$\sqrt{3}$],
故答案为:0;$(-∞,\sqrt{3}]$
点评 本题主要考查分段函数的应用,利用换元法是解决本题的关键.

练习册系列答案
相关题目
15.A和B是抛物线y2=8x上除去原点以外的两个动点,O是坐标原点且满足$\overrightarrow{OA}•\overrightarrow{OB}$=0,$\overrightarrow{OM}•\overrightarrow{AB}$=0,则支动点M的轨迹方程为( )
| A. | x2+y2-8x=0 | B. | y=6x2 | C. | x2+4y2=1 | D. | $\frac{x^2}{9}-\frac{y^2}{4}$=1 |
12.设不等式组$\left\{\begin{array}{l}{x^2}+{y^2}≤1\\ y≥0\end{array}\right.$表示的平面区域为M,不等式组$\left\{\begin{array}{l}0≤x≤t\\ 0≤y≤\sqrt{1-{t^2}}\end{array}\right.$表示的平面区域为N.在M内随机取一个点,这个点在N内的概率的最大值为( )
| A. | $\frac{2}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{π}{4}$ | D. | $\frac{1}{2π}$ |
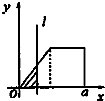
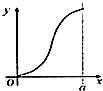 如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )
如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )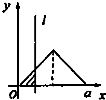
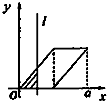
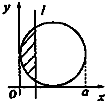
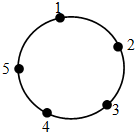 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.