题目内容
13. 如图是一个有底的容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是( )
如图是一个有底的容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是( )| A. | 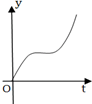 | B. |  | C. | 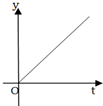 | D. | 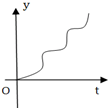 |
分析 判断几何体的形状,根据几何体容器下面粗可得水面高度开始增加的慢,后来增加的快,上面细,然后上面先快后慢得出答案.
解答 解:由三视图,可知几何体是下部是已改圆台,上部是与下部相同倒放的圆台,
因为圆台下面粗,上面细,水面高度开始增加的慢,后来增加的快,
然后上面先快后慢.函数的图象是B.
故选:B.
点评 本题考查了三视图与几何体的关系,函数的图象,要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1.已知数列{an}的通项公式为${a_n}={2^{5-n}}$,数列{bn}的通项公式为bn=n+k,设${c_n}=\left\{\begin{array}{l}{b_n},{a_n}≤{b_n}\\{a_n},{a_n}>{b_n}\end{array}\right.$,若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是( )
| A. | -5≤k≤-4 | B. | -4≤k≤-3 | C. | -5≤k≤-3 | D. | k=-4 |
5.已知函数f(x)=x2-cosx,则$f(\frac{3}{5}),f(0),f(-\frac{1}{2})$的大小关系是( )
| A. | $f(0)<f(\frac{3}{5})<f(-\frac{1}{2})$ | B. | $f(0)<f(-\frac{1}{2})<f(\frac{3}{5})$ | C. | $f(\frac{3}{5})<f(-\frac{1}{2})<f(0)$ | D. | $f(-\frac{1}{2})<f(0)<f(\frac{3}{5})$ |
2.设i为虚数单位,则|1-i|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
3.下列程序框图的功能是寻找使2×4×6×8×…×i>2015成立的i的最小正整数值,则输出框中应填( )
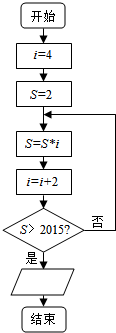

| A. | 输出i-2 | B. | 输出i-1 | C. | 输出i | D. | 输出i+1 |
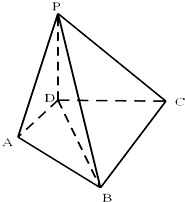 如图所示,PD⊥平面ABCD,AD⊥CD,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图所示,PD⊥平面ABCD,AD⊥CD,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.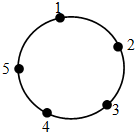 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.