题目内容
(本小题满分12分)
已知函数 =
= ,在
,在 处取得极值2。
处取得极值2。
(1)求函数 的解析式;
的解析式;
(2) 满足什么条件时,区间
满足什么条件时,区间 为函数
为函数 的单调增区间?
的单调增区间?
(3)若 为
为 =
= 图象上的任意一点,直线
图象上的任意一点,直线 与
与 =
= 的图象切于
的图象切于 点,求直线
点,求直线 的斜率的取值范围。
的斜率的取值范围。
已知函数
 =
= ,在
,在 处取得极值2。
处取得极值2。 (1)求函数
 的解析式;
的解析式;(2)
 满足什么条件时,区间
满足什么条件时,区间 为函数
为函数 的单调增区间?
的单调增区间?(3)若
 为
为 =
= 图象上的任意一点,直线
图象上的任意一点,直线 与
与 =
= 的图象切于
的图象切于 点,求直线
点,求直线 的斜率的取值范围。
的斜率的取值范围。(1) (3)
(3)
 (3)
(3)
(1)已知函数 =
= ,
, ,又函数
,又函数 在
在 处取得极值2,
处取得极值2, ,即
,即


(2) 由
所以 的单调增区间为
的单调增区间为 ,
,
若 为函数
为函数 的单调增区间,则有
的单调增区间,则有 解得
解得
即 时,
时, 为函数
为函数 的单调增区间。
的单调增区间。
(3)



直线 的斜率为
的斜率为
令 ,则直线
,则直线 的斜率
的斜率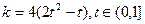 ,
, 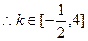 。
。
 =
= ,
, ,又函数
,又函数 在
在 处取得极值2,
处取得极值2, ,即
,即


(2) 由

| x |  |  | (-1,1) | 1 |  |
 | - | 0 | + | 0 | |
 |  | 极小值-2 |  | 极大值2 |  |
 的单调增区间为
的单调增区间为 ,
, 若
 为函数
为函数 的单调增区间,则有
的单调增区间,则有 解得
解得
即
 时,
时, 为函数
为函数 的单调增区间。
的单调增区间。 (3)




直线
 的斜率为
的斜率为
令
 ,则直线
,则直线 的斜率
的斜率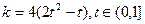 ,
, 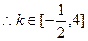 。
。 
练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
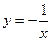 的图象在
的图象在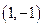 处的切线的方程是( )
处的切线的方程是( )



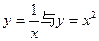 交于点P,过P点的两条切线与x轴分别交于A,B两点,则△ABP的面积为
交于点P,过P点的两条切线与x轴分别交于A,B两点,则△ABP的面积为  是函数
是函数 的一个极值点。⑴求
的一个极值点。⑴求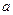 ;⑵求函数
;⑵求函数 的单调区间;⑶若直线
的单调区间;⑶若直线 与函数
与函数 的图象有3个交点,求
的图象有3个交点,求 的取值范围。
的取值范围。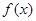 在定义域内可导,
在定义域内可导,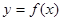 的图象如下右图所示,则导函数
的图象如下右图所示,则导函数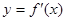 可能为( )
可能为( ) 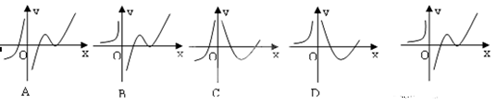
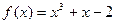 在图象上点P处的切线垂直于直线
在图象上点P处的切线垂直于直线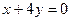 ,则P点的横坐标为( )
,则P点的横坐标为( ) 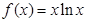 ,若
,若 ,则
,则 ( )
( )



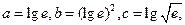 则
则


