题目内容
(本小题满分12分)已知 是函数
是函数 的一个极值点。⑴求
的一个极值点。⑴求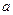 ;⑵求函数
;⑵求函数 的单调区间;⑶若直线
的单调区间;⑶若直线 与函数
与函数 的图象有3个交点,求
的图象有3个交点,求 的取值范围。
的取值范围。
 是函数
是函数 的一个极值点。⑴求
的一个极值点。⑴求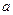 ;⑵求函数
;⑵求函数 的单调区间;⑶若直线
的单调区间;⑶若直线 与函数
与函数 的图象有3个交点,求
的图象有3个交点,求 的取值范围。
的取值范围。(Ⅰ)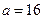 (Ⅱ)
(Ⅱ)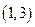 (Ⅲ)
(Ⅲ) 的取值范围为
的取值范围为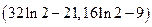
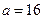 (Ⅱ)
(Ⅱ)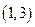 (Ⅲ)
(Ⅲ) 的取值范围为
的取值范围为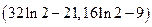
(Ⅰ)因为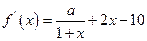 所以
所以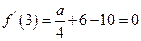 , 因此
, 因此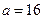 (3分)
(3分)
(Ⅱ)由(Ⅰ)知,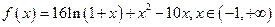
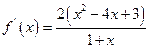 (5分)
(5分)
当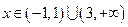 时,
时,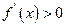 当
当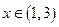 时,
时,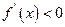
所以 的单调增区间是
的单调增区间是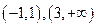
 的单调减区间是
的单调减区间是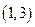 (7分)
(7分)
(Ⅲ)由(Ⅱ)知, 在
在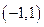 内单调增加,在
内单调增加,在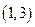 内单调减少,在
内单调减少,在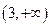 上单调增加,且当
上单调增加,且当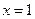 或
或 时,
时,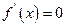 (8分)
(8分)
所以 的极大值为
的极大值为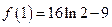 ,极小值为
,极小值为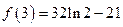
因此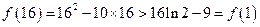
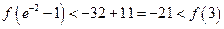
 (10分)
(10分)
所以在 的三个单调区间
的三个单调区间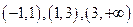 直线
直线 有
有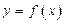 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当 因此,
因此, 的取值范围为
的取值范围为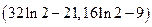 。 (12分)
。 (12分)
评析:此题重点考察利用求导研究函数的单调性,最值问题,函数根的问题;熟悉函数的求导公式,理解求导在函数最值中的研究方法是解题的关键,数形结合理解函数的取值范围。
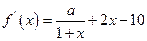 所以
所以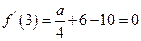 , 因此
, 因此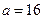 (3分)
(3分)(Ⅱ)由(Ⅰ)知,
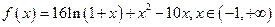
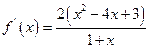 (5分)
(5分)当
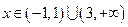 时,
时,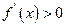 当
当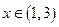 时,
时,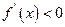
所以
 的单调增区间是
的单调增区间是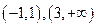
 的单调减区间是
的单调减区间是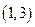 (7分)
(7分)(Ⅲ)由(Ⅱ)知,
 在
在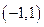 内单调增加,在
内单调增加,在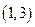 内单调减少,在
内单调减少,在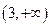 上单调增加,且当
上单调增加,且当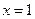 或
或 时,
时,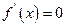 (8分)
(8分)所以
 的极大值为
的极大值为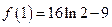 ,极小值为
,极小值为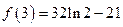
因此
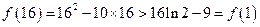
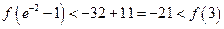
 (10分)
(10分)所以在
 的三个单调区间
的三个单调区间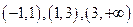 直线
直线 有
有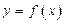 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当 因此,
因此, 的取值范围为
的取值范围为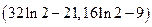 。 (12分)
。 (12分)评析:此题重点考察利用求导研究函数的单调性,最值问题,函数根的问题;熟悉函数的求导公式,理解求导在函数最值中的研究方法是解题的关键,数形结合理解函数的取值范围。

练习册系列答案
相关题目
 .
.
 其中a >0,上存在极值,求实数a的取值范围;
其中a >0,上存在极值,求实数a的取值范围; 时,不等式
时,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. 的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设高为
的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设高为 ,所做成的盒子体积为
,所做成的盒子体积为 (不计接缝)。
(不计接缝)。 为多少时,体积
为多少时,体积
 =
= ,在
,在 处取得极值2。
处取得极值2。  满足什么条件时,区间
满足什么条件时,区间 为函数
为函数 为
为 图象上的任意一点,直线
图象上的任意一点,直线 与
与 点,求直线
点,求直线 有两个极值点
有两个极值点 ,且
,且
 的取值范围,并讨论
的取值范围,并讨论 的单调性;
的单调性;


 在点
在点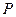 处切线的斜率为
处切线的斜率为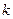 ,当
,当 时,点
时,点 在
在 处取极值,则
处取极值,则