Question

【题目】设抛物线C：y2=2px（p＞0）的焦点为F，点M在C上，|MF|=5，若以MF为直径的圆过点（0，2），则C的方程为（ ）
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x

Answer 1

【答案】C
【解析】解：∵抛物线C方程为y2=2px（p＞0），
∴焦点F坐标为（ ，0），可得|OF|= ，
∵以MF为直径的圆过点（0，2），
∴设A（0，2），可得AF⊥AM，
Rt△AOF中，|AF|= = ，
∴sin∠OAF= = ，
∵根据抛物线的定义，得直线AO切以MF为直径的圆于A点，
∴∠OAF=∠AMF，可得Rt△AMF中，sin∠AMF= = ，
∵|MF|=5，|AF|=
∴ = ，整理得4+ = ，解之可得p=2或p=8
因此，抛物线C的方程为y2=4x或y2=16x．
故选：C．
方法二：
∵抛物线C方程为y2=2px（p＞0），∴焦点F（ ，0），
设M（x，y），由抛物线性质|MF|=x+ =5，可得x=5﹣ ，
因为圆心是MF的中点，所以根据中点坐标公式可得，圆心横坐标为 = ，
由已知圆半径也为 ，据此可知该圆与y轴相切于点（0，2），故圆心纵坐标为2，则M点纵坐标为4，
即M（5﹣ ，4），代入抛物线方程得p2﹣10p+16=0，所以p=2或p=8．
所以抛物线C的方程为y2=4x或y2=16x．
故答案C．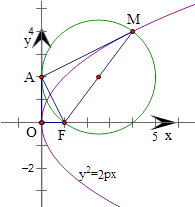

根据抛物线方程算出|OF|= ，设以MF为直径的圆过点A（0，2），在Rt△AOF中利用勾股定理算出|AF|= ．再由直线AO与以MF为直径的圆相切得到∠OAF=∠AMF，Rt△AMF中利用∠AMF的正弦建立关系式，从而得到关于p的方程，解之得到实数p的值，进而得到抛物线C的方程．