Question

【题目】在中，已知，，，为线段上的一点，且，则的最小值为（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】分析：△ABC中设AB=c，BC=a，AC=b，由sinB=cosAsinC结合三角形的内角和及和角的正弦公式化简可求 cosC=0 即C=90°，再由，S△ABC=6可得bccosA=9，可求得c=5，b=3，a=4，考虑建立以AC所在的直线为x轴，以BC所在的直线为y轴建立直角坐标系，由P为线段AB上的一点，则存在实数λ使得=（3λ，4﹣4λ）（0≤λ≤1），设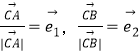则，，由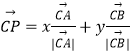=（x，0）+（0，y）=（x，y）可得x=3λ，y=4﹣4λ则4x+3y=12而，利用基本不等式求解最小值．

详解：△ABC中设AB=c，BC=a，AC=b

∵sinB=cosAsinC，∴sin（A+C）=sinCcosA，

即sinAcosC+sinCcosA=sinCcosA，

∴sinAcosC=0，

∵sinA≠0，∴cosC=0 C=90°

∵，S△ABC=6

∴bccosA=9，

∴，根据直角三角形可得sinA=，cosA=，bc=15

∴c=5，b=3，a=4

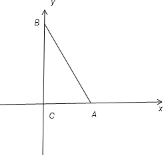
以AC所在的直线为x轴，以BC所在的直线为y轴建立直角坐标系可得C（0，0）A（3，0）B（0，4）

P为线段AB上的一点，则存在实数λ使得=（3λ，4﹣4λ）（0≤λ≤1）

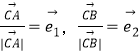设，则，

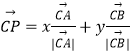∴=（x，0）+（0，y）=（x，y）

∴x=3λ，y=4﹣4λ则4x+3y=12

=

故所求的最小值为

故选：C．