Question

【题目】如图，在三棱锥中，平面平面，，，，为的中点.

（1）证明：平面；

（2）求二面角的余弦值.

Answer 1

【答案】(1)证明见解析.

(2).

【解析】分析：（1）证，.即可由线面垂的判定定理得出结论；

（2）通过建系，分别求出面DSC和面SCA的法向量，进行计算，观察图中二面角的范围得出余弦值的符号

（1）证明：因为平面平面，平面平面，且，

所以平面，所以.

又因为，，所以，即.

因为，且平面，

所以平面.

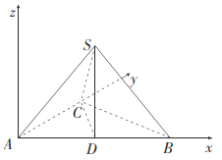
（2）解：如图，建立空间直角坐标系，令，则，，，，.

易得，，.

设为平面的一个法向量，则

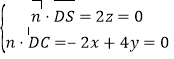，取，则，，

所以.

又因为为平面的一个法向量，所以.

所以二面角的余弦值为.

点晴：空间立体是高考必考的解答题之一，在做这类题目时，正面题大家需要注意书写的步骤分，判定定理的必要点必须要有；另外在求角等问题时我们可以利用向量法进行解决问题，注意角的范围问题。