题目内容
已知函数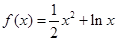 .
.
(1)求函数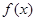 在区间
在区间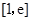 上的最大、最小值;
上的最大、最小值;
(2)求证:在区间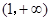 上,函数
上,函数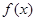 的图象在函数
的图象在函数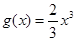 的图象的下方.
的图象的下方.
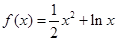 .
.(1)求函数
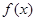 在区间
在区间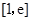 上的最大、最小值;
上的最大、最小值;(2)求证:在区间
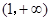 上,函数
上,函数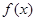 的图象在函数
的图象在函数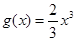 的图象的下方.
的图象的下方.(1)函数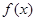 在区间
在区间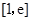 上的最大值为
上的最大值为 ,最小值为
,最小值为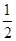 ;
;
(2)要证明在区间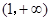 上,函数
上,函数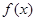 的图象在函数
的图象在函数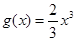 的图象的下方,只要证明前者的最小值大于后者的最大值即可。
的图象的下方,只要证明前者的最小值大于后者的最大值即可。
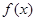 在区间
在区间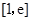 上的最大值为
上的最大值为 ,最小值为
,最小值为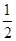 ;
;(2)要证明在区间
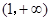 上,函数
上,函数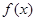 的图象在函数
的图象在函数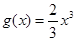 的图象的下方,只要证明前者的最小值大于后者的最大值即可。
的图象的下方,只要证明前者的最小值大于后者的最大值即可。试题分析:解:(1)由已知
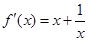 , 1分
, 1分当
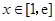 时,
时,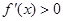 ,所以函数
,所以函数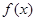 在区间
在区间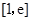 上单调递增, 3分
上单调递增, 3分所以函数
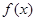 在区间
在区间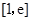 上的最大、最小值分别为
上的最大、最小值分别为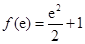 ,
,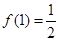 ,所以函数
,所以函数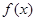 在区间
在区间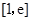 上的最大值为
上的最大值为 ,最小值为
,最小值为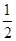 ; 6分
; 6分(2)证明:设
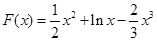 ,则
,则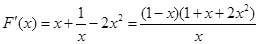 .…8分
.…8分因为
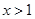 ,所以
,所以 ,所以函数
,所以函数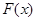 在区间
在区间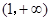 上单调递减, ……9分
上单调递减, ……9分又
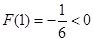 ,所以在区间
,所以在区间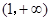 上,
上,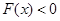 ,即
,即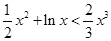 ,
,所以在区间
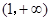 上函数
上函数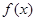 的图象在函数
的图象在函数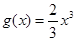 图象的下方.………13分
图象的下方.………13分点评:解决的关键是利用导数的符号判定函数单调性,并能结合极值得到最值,进而得到图象之间的关系,属于基础题。

练习册系列答案
相关题目
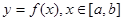 ,其导函数的图象如图所示,则函数
,其导函数的图象如图所示,则函数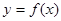 的减区间是
的减区间是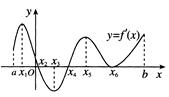




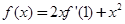 ,则
,则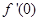 等于 ( )
等于 ( )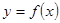 是下列的( )时,f ′(x)一定是增函数。
是下列的( )时,f ′(x)一定是增函数。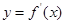 的图象,则下列命题错误的是( )
的图象,则下列命题错误的是( )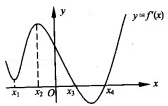
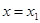 处有极小值
处有极小值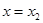 处有极大值
处有极大值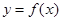 在
在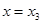 处有极小值
处有极小值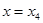 处有极小值
处有极小值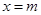 与函数
与函数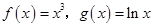 的图象分别交于点
的图象分别交于点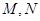 。则
。则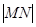 的最小值为( )
的最小值为( )



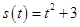 (
(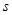 单位:
单位: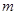 ,
,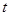 单位:
单位: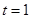 时的瞬时速度为( )
时的瞬时速度为( )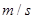
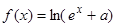 是实数集R上的奇函数,且
是实数集R上的奇函数,且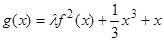 在R上为增函数。
在R上为增函数。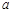 的值;
的值;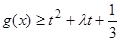 在
在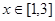 恒成立时的实数t的取值范围。
恒成立时的实数t的取值范围。 在
在 处切线的斜率是 .
处切线的斜率是 .