Question

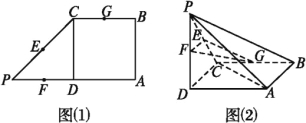
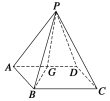
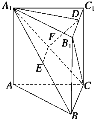
【题目】如图所示，P是四边形ABCD所在平面外的一点，四边形ABCD是∠DAB＝60°且边长为a的菱形．侧面PAD为正三角形，其所在平面垂直于底面ABCD．

（1）若G为AD边的中点，求证：BG⊥平面PAD；

（2）求证：AD⊥PB．

Answer 1

【答案】（1）详见解析（2）详见解析

【解析】

试题分析：（1）连接BD，根据条件可知△ABD是正三角形，而G为AD边的中点，则BG⊥AD，BG平面ABCD又平面APD⊥平面ABCD，平面APD∩平面ABCD=AD，根据面面垂直的性质定理可知BG⊥平面APD；（2）连接PG，由侧面PAD为正三角形，G为AD边的中点得到AD⊥PG，再由（1）可知BG⊥AD，PG，BG平面PBG，PG∩BG=G，根据线面垂直的判定定理可知AD⊥平面PBG，而PB平面PBG，根据线面垂直的性质可知AD⊥PB

试题解析：（1）连结PG，由题知△PAD为正三角形，G是AD的中点，∴PG⊥AD．

又平面PAD⊥平面ABCD，∴PG⊥平面ABCD，∴PG⊥BG．

又∵四边形ABCD是菱形且∠DAB＝60°，∴BG⊥AD．

又AD∩PG＝G，∴BG⊥平面PAD．

（2）由（1）可知BG⊥AD，PG⊥AD．

所以AD⊥平面PBG，所以AD⊥PB．