题目内容
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
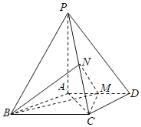
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N-BCM的体积.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(1)取BC中点E,连结EN,EM。易得四边形ABEM是平行四边形,进而平面NEM∥平面PAB,∴MN∥平面PAB.(2)设AC中点F,则VN-BCM=![]() 。求出S△BCM面积,算S△BCM面积时高时构造一个等高的△MEG ,NF=
。求出S△BCM面积,算S△BCM面积时高时构造一个等高的△MEG ,NF=![]() PA=2,带入即可。
PA=2,带入即可。
(Ⅰ)取BC中点E,连结EN,EM,∵N为PC的中点,∴NE是△PBC的中位线
∴NE∥PB,又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE=![]() BC=AM=2,∴四边形ABEM是平行四边形,
BC=AM=2,∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,∵MN平面NEM,∴MN∥平面PAB.
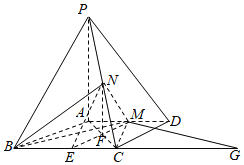
(Ⅱ)取AC中点F,连结NF,∵NF是△PAC的中位线,∴NF∥PA,NF=![]() PA=2,
PA=2,
又∵PA⊥面ABCD,∴NF⊥面ABCD,如图,延长BC至G,使得CG=AM,连结GM,
∵AM![]() CG,∴四边形AGCM是平行四边形,∴AC=MG=3,
CG,∴四边形AGCM是平行四边形,∴AC=MG=3,
又∵ME=3,EC=CG=2,∴△MEG的高h=![]() ,
,
∴S△BCM=![]() ×BC×h=
×BC×h=![]() ×4×
×4×![]() =2
=2![]() ,
,
∴四面体N-BCM的体积VN-BCM=![]() .
.

【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元。
(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得下表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望。
【题目】甲、乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台机床生产的零件各100件进行检测,检测结果统计如下:
测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
甲机床 | 8 | 12 | 40 | 32 | 8 |
乙机床 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产1件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元,假设甲机床某天生产50件零件,请估计甲机床该天的利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任意抽取2件进行质量分析,求这2件都是乙机床生产的概率.


