题目内容
17.设函数f(x)=(x-t)lnx-1(t∈R,t为常数),已知f(x)在x=1处的切线平行于x轴.(Ⅰ)求常数t的值;
(Ⅱ)(i)证明函数f(x)恰有两个零点x1<x2;
(ii)设g(x)=f(x)+lnx+1,是否存在最小的正常数m,使得:当a>m时,对于任意正实数x,不等式g(x+a)<g(a)ex恒成立?
分析 (Ⅰ)求出f(x)的导数,求得切线的斜率,代入x=1可得切线的斜率为0,解方程可得t=1;
(Ⅱ)(i)求出函数的导数,判断函数的单调性,运用零点存在定理,即可判断零点个数;
(ii)这样的最小正常数m存在.由g(x)=f(x)-lnx-1=xlnx,由g(x+a)<g(a)ex得(a+x)ln(a+x)<alna•ex即$\frac{{({a+x})ln({a+x})}}{{{e^{x+a}}}}<\frac{alna}{e^a}$,设$h(x)=\frac{xlnx}{e^x}$,则问题就是否存在最小的正常数m,使得当a>m时,对于任意正实数x,不等式h(x+a)<h(a)恒成立.求出h(x)的导数,求得单调区间,极值、最值,运用单调性即可判断.
解答 解:(Ⅰ)由f(x)=(x-t)lnx-1得$f'(x)=\frac{x-t}{x}+lnx$,
由f(x)在x=1处的切线平行于x轴知,f'(1)=1-t=0,
所以t=1.
(Ⅱ)(i)证明:由(Ⅰ)知t=1,所以$f'(x)=\frac{x-1}{x}+lnx$,
所以$f''(x)=\frac{1}{x^2}+\frac{1}{x}>0$,
所以f'(x)是增函数,又因为f'(1)=0,
所以当x∈(0,1)时f'(x)<f'(1)=0,所以f(x)在(0,1)上单调递减,
当x∈(1,+∞)时f′(x)>f′(1)=0,所以f(x)在(1,+∞)上单调递增,
又因为$f({\frac{1}{e^2}})=({\frac{1}{e^2}-1})ln\frac{1}{e^2}-1=1-\frac{2}{e^2}>0,f(1)=-1<0,f(e)=({e-1})lne-1=e-2>0$,
即$f({\frac{1}{e^2}})f(1)<0,f(1)f(e)<0$,
所以f(x)在(0,1)和(1,+∞)上各有一个零点,
即函数f(x)恰有两个零点x1<x2,且满足0<x1<1<x2<e.
(ii)这样的最小正常数m存在.
理由:g(x)=f(x)-lnx-1=xlnx,
所以由g(x+a)<g(a)ex得(a+x)ln(a+x)<alna•ex
即$\frac{{({a+x})ln({a+x})}}{{{e^{x+a}}}}<\frac{alna}{e^a}$,
设$h(x)=\frac{xlnx}{e^x}$,则问题就是否存在最小的正常数m,
使得当a>m时,对于任意正实数x,不等式h(x+a)<h(a)恒成立.
因为$h'(x)=\frac{{({1+lnx}){e^x}-xlnx{e^x}}}{{{e^{2x}}}}=-f(x){e^x}$,
由(i)知f(x)在(0,1)和(1,+∞)上各有一个零点,
即0<x1<1<x2<e,
且f(x)在(0,1)上单调递减,在(1,+∞)上单调递增
所以当x∈(0,x1)时f(x)>0,
h′(x)=-f(x)ex<0,h(x)在(0,x1)上单调递减,
当x∈(x1,x2)时f(x)<0,h'(x)=-f(x)ex>0,
h(x)在(x1,x2)上单调递增.
当x∈(x2,+∞)时f(x)>0,h'(x)=-f(x)ex<0,
h(x)在(x2,+∞)上单调递减.
注意到h(1)=0,当x∈(0,1)时h(x)<0时;
当x∈(1,+∞)时h(x)>0,
则h(x2)是函数的极大值,也是最大值.
题目要找的m=x2,理由是:当a>x2时,对于任意正实数x,x+a>a>x2,
而h(x)在(x2,+∞)上单调递减,
所以h(x+a)<h(a)一定恒成立,说明m≤x2;
另一方面,当0<a<x2,取x=x2-a,显然x>0且h(x+a)=h(x2)>h(a)
题目所要求的不等式不恒成立,说明m不能比x2小.
综上可知,题目所要寻求的最小正常数m就是x2,即存在最小正常数m=x2,
当a>m时,对于任意正实数x,不等式g(x+a)<g(a)ex恒成立.
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,同时考查函数的零点存在定理和函数的单调性的运用,属于中档题.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案| A. | $\frac{{a}^{3}}{4}$ | B. | $\frac{{a}^{3}}{3}$ | C. | $\frac{{a}^{3}}{2}$ | D. | $\frac{3{a}^{3}}{4}$ |
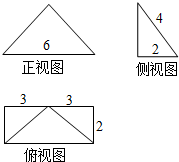
| A. | 48 | B. | 24$\sqrt{3}$ | C. | 16 | D. | 8$\sqrt{3}$ |
 如图是y=f(x)的导函数的图象,现有四种说法:
如图是y=f(x)的导函数的图象,现有四种说法: 如图,长沙河西先导区某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的矩形绿化区,这三块绿化区四周和绿化区之间设有1米宽的走道.已知三块绿化区的总面积为800平方米,则该矩形区域ABCD占地面积的最小值为( )平方米.
如图,长沙河西先导区某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的矩形绿化区,这三块绿化区四周和绿化区之间设有1米宽的走道.已知三块绿化区的总面积为800平方米,则该矩形区域ABCD占地面积的最小值为( )平方米.