题目内容
9.已知a>0,若(x2+1)(ax+1)6的展开式中各项系数的和为1458,则该展开式中x2项的系数为61.分析 根据展开式中各项系数的和求出a的值,再由通项公式Tr+1求出展开式中x2项的系数.
解答 解:根据题意,展开式中各项系数的和是(12+1)(a+1)6=1458,
∴a=2,
(2x+1)6的通项公式是Tr+1=${C}_{6}^{r}$•(2x)r,
∴展开式中x2项的系数是1+${C}_{6}^{2}$×4=61.
故答案为:61.
点评 本题考查了二项式定理的应用问题,解题时应弄清二项式系数、展开式中各项的系数是什么,是基础题.

练习册系列答案
相关题目
19.用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,则该长方体的最大体积为( )
| A. | 2m3 | B. | 3m3 | C. | 4m3 | D. | 5m3 |
1.复数z=$\frac{1-i}{1+i}$,则z2的虚部是( )
| A. | 1 | B. | -1 | C. | i | D. | 0 |
18.执行下面的程序框图,如果输入的N=4,那么输出的S=( )
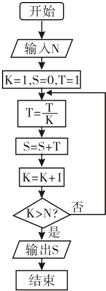

| A. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ | B. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$ | ||
| C. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$+$\frac{1}{5}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$+ |
 如图所示,在平面四边形ABCD中,$\overrightarrow{DA}•\overrightarrow{AB}=0,|{\overrightarrow{EC}}|=\sqrt{7},|{\overrightarrow{AD}}|=3,\overrightarrow{AE}=2\overrightarrow{ED}$,$\overrightarrow{DA}$与$\overrightarrow{DC}$的夹角为$\frac{2}{3}π$,$\overrightarrow{EC}$与$\overrightarrow{EB}$的夹角为$\frac{π}{3}$.
如图所示,在平面四边形ABCD中,$\overrightarrow{DA}•\overrightarrow{AB}=0,|{\overrightarrow{EC}}|=\sqrt{7},|{\overrightarrow{AD}}|=3,\overrightarrow{AE}=2\overrightarrow{ED}$,$\overrightarrow{DA}$与$\overrightarrow{DC}$的夹角为$\frac{2}{3}π$,$\overrightarrow{EC}$与$\overrightarrow{EB}$的夹角为$\frac{π}{3}$.