题目内容
8.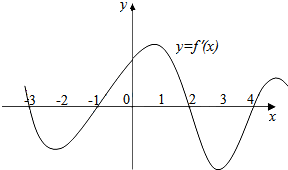 如图是y=f(x)的导函数的图象,现有四种说法:
如图是y=f(x)的导函数的图象,现有四种说法:(1)f(x)在(-2,1)上是增函数;
(2)x=-1是f(x)的极小值点;
(3)f(x)在(-1,2)上是增函数;
(4)x=2是f(x)的极小值点;
以上说法正确的序号是(2),(3).
分析 利用函数的导数的图象,对选项逐一判断即可.
解答 解:由函数的图象可知:f′(-2)<0,f′(-1)=0,f(x)在(-2,1)上是增函数,(1)不正确;
x=-1时f′(1)=0,函数在(-3,-1)递减,在(-1,2)递增,x=-1是f(x)的极小值点;所以(2)正确;
f(x)在(-1,2)上f′(x)>0,函数是增函数,所以(3)正确;
函数在(-1,2)递增,在(2,4)递减,x=2是f(x)的极大值点,所以D不正确.
故答案为:(2),(3)
点评 本题考查函数的图象的应用,导数与函数的图象的区别,函数的极值以及函数的单调性的判断,基本知识的考查.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
19.用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,则该长方体的最大体积为( )
| A. | 2m3 | B. | 3m3 | C. | 4m3 | D. | 5m3 |
16.已知复数z满足$\frac{2-i}{z}$=1+2i,则$\overrightarrow{z}$=( )
| A. | 4+3i | B. | 4-3i | C. | -i | D. | i |
3.方程$\frac{x^2}{4+m}+\frac{y^2}{2-m}=1$表示椭圆的必要不充分条件是( )
| A. | m∈(-1,2) | B. | m∈(-4,2) | C. | m∈(-4,-1)∪(-1,2) | D. | m∈(-1,+∞) |
18.执行下面的程序框图,如果输入的N=4,那么输出的S=( )
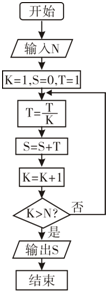

| A. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ | B. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$ | ||
| C. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$+$\frac{1}{5}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$+ |