题目内容
12．如图是某四棱锥的三视图，则该棱锥的体积是 （ ）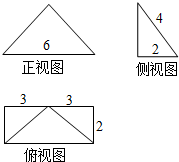
| A． | 48 | B． | 24$\sqrt{3}$ | C． | 16 | D． | 8$\sqrt{3}$ |
分析 一个底面是矩形的四棱锥，矩形的长和宽分别是6，2，底面上的高与底面交于底面一条边的中点，四棱锥的高是2$\sqrt{3}$，即可求解．
解答 解：由三视图知，这是一个底面是矩形的四棱锥，
矩形的长和宽分别是6，2
底面上的高与底面交于底面一条边的中点，
四棱锥的高是$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$，
∴四棱锥的体积为：$\frac{1}{3}$×2×6×2$\sqrt{3}$=8$\sqrt{3}$．
故选：D
点评 本题考查由三视图求几何体的体积，考查由三视图还原几何体的直观图，考查平面图形体积的求法，本题是一个基础题．
练习册系列答案
相关题目
2．将x=2输入以下程序框图（如图），得结果为（ ）
| A． | 3 | B． | 5 | C． | 8 | D． | 12 |
3．方程$\frac{x^2}{4+m}+\frac{y^2}{2-m}=1$表示椭圆的必要不充分条件是（ ）
| A． | m∈（-1，2） | B． | m∈（-4，2） | C． | m∈（-4，-1）∪（-1，2） | D． | m∈（-1，+∞） |
如图所示，在平面四边形ABCD中，$\overrightarrow{DA}•\overrightarrow{AB}=0，|{\overrightarrow{EC}}|=\sqrt{7}，|{\overrightarrow{AD}}|=3，\overrightarrow{AE}=2\overrightarrow{ED}$，$\overrightarrow{DA}$与$\overrightarrow{DC}$的夹角为$\frac{2}{3}π$，$\overrightarrow{EC}$与$\overrightarrow{EB}$的夹角为$\frac{π}{3}$．
1．复数z=$\frac{1-i}{1+i}$，则z2的虚部是（ ）
| A． | 1 | B． | -1 | C． | i | D． | 0 |