题目内容
6.化简$\frac{sin(kπ-α)cos(kπ+α)}{sin[(k+1)π+α]cos[(k+1)π-α]}$=-1.分析 分类讨论,利用诱导公式,即可得出结论.
解答 解:k是偶数时,$\frac{sin(kπ-α)cos(kπ+α)}{sin[(k+1)π+α]cos[(k+1)π-α]}$=$\frac{-sinαcosα}{-sinα(-cosα)}$=-1;
k是奇数时,$\frac{sin(kπ-α)cos(kπ+α)}{sin[(k+1)π+α]cos[(k+1)π-α]}$=$\frac{sinα(-cosα)}{sinαcosα}$=-1.
故答案为:-1.
点评 本题考查诱导公式的运用,考查分类讨论的数学思想,考查学生的计算能力,比较基础.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
16.已知复数z满足$\frac{2-i}{z}$=1+2i,则$\overrightarrow{z}$=( )
| A. | 4+3i | B. | 4-3i | C. | -i | D. | i |
1.复数z=$\frac{1-i}{1+i}$,则z2的虚部是( )
| A. | 1 | B. | -1 | C. | i | D. | 0 |
18.执行下面的程序框图,如果输入的N=4,那么输出的S=( )
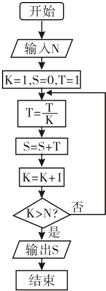

| A. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ | B. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$ | ||
| C. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$+$\frac{1}{5}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$+ |
15.下列四个命题:
(1)“?x∈R,2x+5>0”是全称命题;
(2)命题“?x∈R,x2+5x=6”的否定是“?x0∉R,使x02+5x0≠6”;
(3)若|x|=|y|,则x=y;
(4)若p∨q为假命题,则p、q均为假命题.
其中真命题的序号是( )
(1)“?x∈R,2x+5>0”是全称命题;
(2)命题“?x∈R,x2+5x=6”的否定是“?x0∉R,使x02+5x0≠6”;
(3)若|x|=|y|,则x=y;
(4)若p∨q为假命题,则p、q均为假命题.
其中真命题的序号是( )
| A. | (1)(2) | B. | (2)(4) | C. | (1)(4) | D. | (1)(2)(3)(4) |
