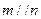题目内容
(本小题满分14分)如图,在四棱锥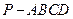 中,底面
中,底面 是边长为
是边长为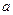 的正方形,
的正方形,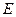 、
、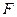 分别为
分别为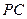 、
、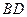 的中点,侧面
的中点,侧面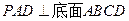 ,且
,且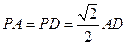 .
.
(1)求证: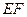 ∥平面
∥平面 ;(2)求三棱锥
;(2)求三棱锥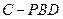 的体积.
的体积. 
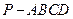 中,底面
中,底面 是边长为
是边长为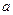 的正方形,
的正方形,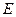 、
、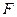 分别为
分别为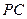 、
、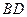 的中点,侧面
的中点,侧面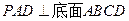 ,且
,且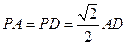 .
.(1)求证:
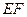 ∥平面
∥平面 ;(2)求三棱锥
;(2)求三棱锥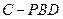 的体积.
的体积. 
解:(1)证明:连结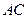 ,则
,则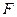 是
是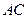 的中点,
的中点,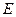 为
为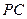 的中点
的中点
故在△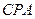 中,
中, 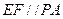 , …………3分
, …………3分
且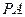
 平面PAD,
平面PAD,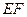
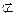 平面PAD,∴
平面PAD,∴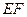 ∥平面PAD …………6分
∥平面PAD …………6分
(2)取 的中点M,连结
的中点M,连结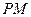 ,
,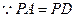 ,
,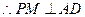 …………8分
…………8分
又平面 ⊥平面
⊥平面 , 平面
, 平面 ∩平面
∩平面 =
= ,
,
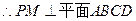 , ……………10分
, ……………10分
 ……………14分
……………14分
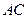 ,则
,则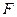 是
是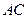 的中点,
的中点,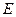 为
为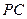 的中点
的中点故在△
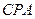 中,
中, 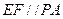 , …………3分
, …………3分且
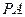
 平面PAD,
平面PAD,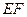
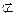 平面PAD,∴
平面PAD,∴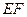 ∥平面PAD …………6分
∥平面PAD …………6分(2)取
 的中点M,连结
的中点M,连结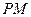 ,
,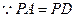 ,
,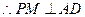 …………8分
…………8分又平面
 ⊥平面
⊥平面 , 平面
, 平面 ∩平面
∩平面 =
= ,
,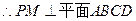 , ……………10分
, ……………10分 ……………14分
……………14分略

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 平面
平面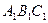 ,
,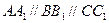 ,且
,且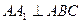 ,
,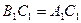 ,
,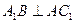 ,求证:
,求证: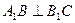
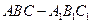 中,侧棱
中,侧棱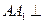 底面
底面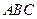 ,
,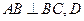 为
为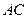 的中点,
的中点,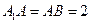 .
.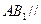 平面
平面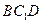 ;
;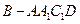 的体积为
的体积为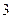 ,求二面角
,求二面角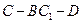 的正切值.
的正切值. 图5
图5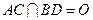 .将正方形ABCD沿对角线
.将正方形ABCD沿对角线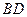 折起,使
折起,使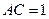 ,得到三棱锥A—BCD,如图所示.
,得到三棱锥A—BCD,如图所示.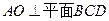 ;
;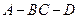 的余弦值.
的余弦值.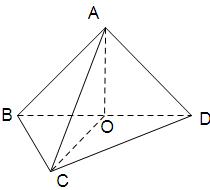

 中,AC="BC," AC⊥BC,点D是A1B1中点.
中,AC="BC," AC⊥BC,点D是A1B1中点.  ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.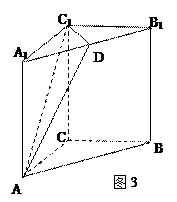
 中,
中, ,
, 平面
平面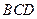 ,
,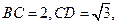
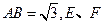 分别为
分别为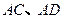 上的动点.
上的动点.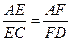 ,求证:平面
,求证:平面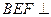 平面
平面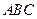 ;
;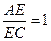 ,
,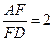 ,求平面
,求平面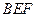 与平面
与平面
 C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是( )
C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是( )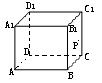
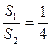 ,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则 ;
;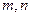 是两条不同的直线,
是两条不同的直线,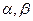 是两个不同的平面,
是两个不同的平面, 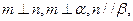 则
则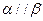
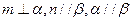 ,则
,则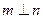
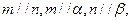 则
则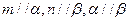 ,则
,则