题目内容
在平面几何中有如下结论:正三角形ABC的内切圆面积为S1,外接圆面积为S2,则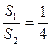 ,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则 ;
;
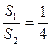 ,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则 ;
;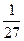
略

练习册系列答案
相关题目
题目内容
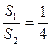 ,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则
,推广到空间可以得到类似结论;已知正四面体P—ABC的内切球体积为V1,外接球体积为V2,则 ;
;