题目内容
(本小题满分14分)
如图5,在三棱柱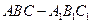 中,侧棱
中,侧棱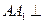 底面
底面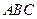 ,
,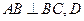 为
为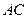 的中点,
的中点,
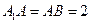 .
.
(1) 求证: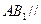 平面
平面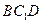 ;
;
(2)若四棱锥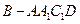 的体积为
的体积为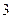 ,求二面角
,求二面角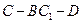 的正切值.
的正切值.
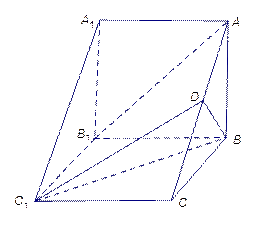 图5
图5
如图5,在三棱柱
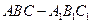 中,侧棱
中,侧棱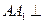 底面
底面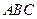 ,
,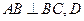 为
为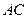 的中点,
的中点,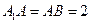 .
.(1) 求证:
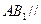 平面
平面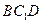 ;
;(2)若四棱锥
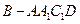 的体积为
的体积为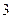 ,求二面角
,求二面角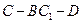 的正切值.
的正切值. 图5
图5(本小题主要考查空间线面关系、二面角的平面角、锥体的体积等知识, 考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)
(1)证明:连接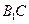 ,设
,设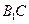 与
与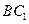 相交于点
相交于点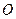 ,连接
,连接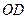 ,
,
∵ 四边形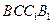 是平行四边形,
是平行四边形,
 ∴点
∴点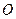 为
为 的中点.
的中点.
∵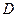 为
为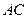 的中点,
的中点,
∴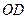 为△
为△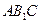 的中位线,
的中位线,
∴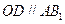 . …… 2分
. …… 2分
∵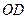
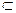 平面
平面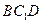 ,
,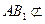 平面
平面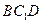 ,
,
∴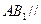 平面
平面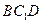 . …… 4分
. …… 4分
(2)解: 依题意知,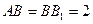 ,
,
∵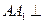 平面
平面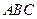 ,
,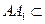 平面
平面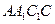 ,
,
∴ 平面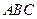
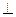 平面
平面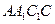 ,且平面
,且平面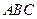
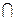 平面
平面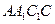
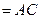 .
.
作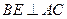 ,垂足为
,垂足为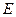 ,则
,则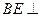 平面
平面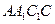 , ……6分
, ……6分
设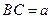 ,
,
在Rt△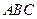 中,
中,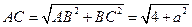 ,
,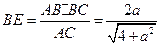 ,
,
∴四棱锥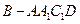 的体积
的体积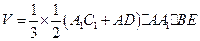
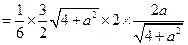
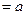 . …… 8分
. …… 8分
依题意得,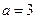 ,即
,即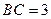 . …… 9分
. …… 9分
(以下求二面角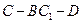 的正切值提供两种解法)
的正切值提供两种解法)
解法1:∵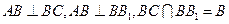 ,
,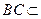 平面
平面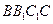 ,
,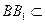 平面
平面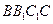 ,
,
∴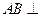 平面
平面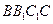 .
.
取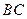 的中点
的中点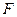 ,连接
,连接 ,则
,则
 ,且
,且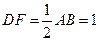 .
.
∴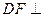 平面
平面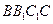 .
.
作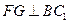 ,垂足为
,垂足为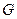 ,连接
,连接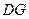 ,
,
由于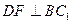 ,且
,且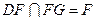 ,
,
∴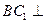 平面
平面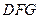 .
.
∵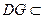 平面
平面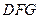 ,
,
∴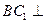
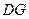 .
.
∴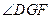 为二面角
为二面角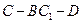 的平面角. …… 12分
的平面角. …… 12分
由Rt△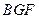 ~Rt△
~Rt△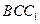 ,得
,得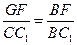 ,
,
得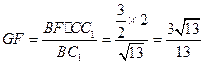 ,
,
在Rt△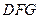 中,
中, 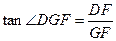
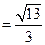 .
.
∴二面角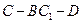 的正切值为
的正切值为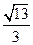 . …… 14分
. …… 14分
解法2: ∵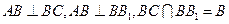 ,
,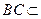 平面
平面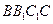 ,
,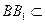 平面
平面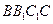 ,
,
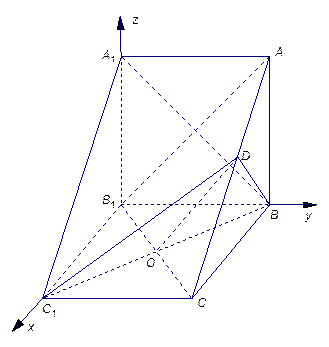 ∴
∴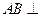 平面
平面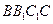 .
.
以点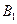 为坐标原点,分别以
为坐标原点,分别以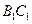 ,
,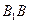 ,
,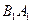 所在直线为
所在直线为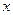 轴,
轴,
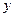 轴和
轴和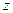 轴,建立空间直角坐标系
轴,建立空间直角坐标系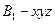 .
.
则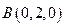 ,
,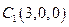 ,
,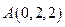 ,
,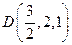 .
.
∴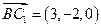 ,
,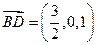
设平面 的法向量为
的法向量为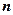
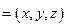 ,
,
由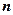
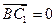 及
及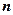
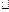
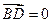 ,得
,得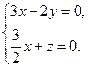
令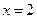 ,得
,得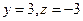 .
.
故平面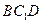 的一个法向量为
的一个法向量为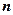
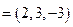 , …… 11分
, …… 11分
又平面 的一个法向量为
的一个法向量为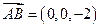 ,
,
∴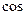
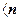 ,
,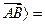
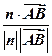
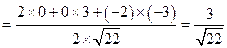 . …… 12分
. …… 12分
∴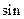
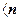 ,
,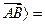
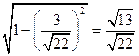 . …… 13分
. …… 13分
∴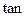
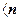 ,
,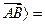
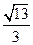 .
.
∴二面角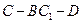 的正切值为
的正切值为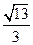 . …… 14分
. …… 14分
(1)证明:连接
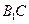 ,设
,设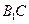 与
与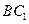 相交于点
相交于点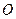 ,连接
,连接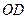 ,
,∵ 四边形
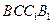 是平行四边形,
是平行四边形, ∴点
∴点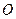 为
为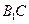 的中点.
的中点. ∵
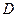 为
为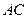 的中点,
的中点,∴
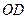 为△
为△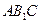 的中位线,
的中位线,∴
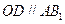 . …… 2分
. …… 2分∵
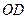
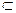 平面
平面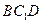 ,
,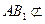 平面
平面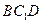 ,
,∴
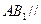 平面
平面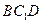 . …… 4分
. …… 4分(2)解: 依题意知,
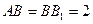 ,
,∵
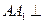 平面
平面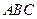 ,
,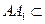 平面
平面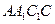 ,
,∴ 平面
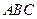
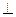 平面
平面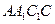 ,且平面
,且平面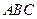
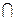 平面
平面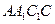
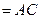 .
.作
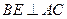 ,垂足为
,垂足为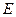 ,则
,则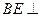 平面
平面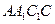 , ……6分
, ……6分设
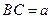 ,
,在Rt△
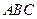 中,
中,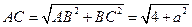 ,
,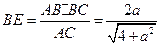 ,
,∴四棱锥
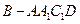 的体积
的体积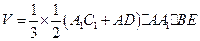
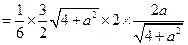
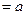 . …… 8分
. …… 8分依题意得,
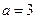 ,即
,即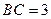 . …… 9分
. …… 9分(以下求二面角
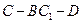 的正切值提供两种解法)
的正切值提供两种解法)解法1:∵
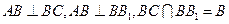 ,
,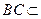 平面
平面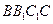 ,
,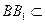 平面
平面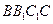 ,
,∴
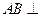 平面
平面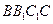 .
.取
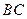 的中点
的中点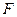 ,连接
,连接 ,则
,则
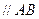 ,且
,且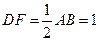 .
.∴
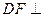 平面
平面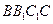 .
.作
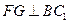 ,垂足为
,垂足为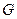 ,连接
,连接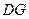 ,
,由于
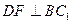 ,且
,且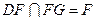 ,
,∴
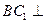 平面
平面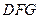 .
.∵
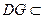 平面
平面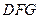 ,
,∴
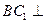
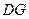 .
.∴
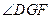 为二面角
为二面角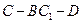 的平面角. …… 12分
的平面角. …… 12分由Rt△
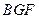 ~Rt△
~Rt△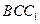 ,得
,得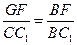 ,
,得
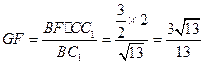 ,
,在Rt△
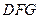 中,
中, 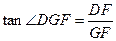
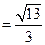 .
.∴二面角
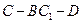 的正切值为
的正切值为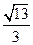 . …… 14分
. …… 14分解法2: ∵
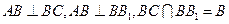 ,
,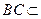 平面
平面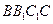 ,
,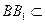 平面
平面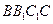 ,
, ∴
∴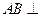 平面
平面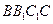 .
.以点
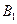 为坐标原点,分别以
为坐标原点,分别以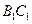 ,
,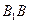 ,
,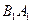 所在直线为
所在直线为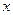 轴,
轴,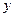 轴和
轴和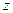 轴,建立空间直角坐标系
轴,建立空间直角坐标系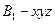 .
.则
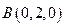 ,
,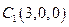 ,
,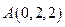 ,
,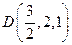 .
.∴
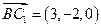 ,
,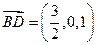
设平面
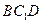 的法向量为
的法向量为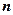
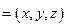 ,
, 由
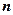
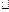
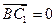 及
及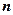
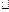
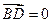 ,得
,得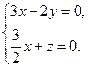
令
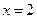 ,得
,得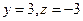 .
.故平面
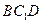 的一个法向量为
的一个法向量为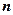
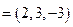 , …… 11分
, …… 11分又平面
 的一个法向量为
的一个法向量为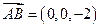 ,
,∴
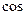
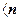 ,
,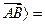
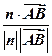
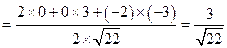 . …… 12分
. …… 12分∴
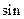
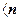 ,
,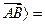
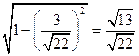 . …… 13分
. …… 13分∴
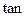
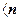 ,
,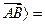
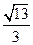 .
.∴二面角
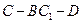 的正切值为
的正切值为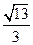 . …… 14分
. …… 14分略

练习册系列答案
相关题目
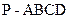 中,
中,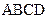 是矩形,侧棱PD⊥底面
是矩形,侧棱PD⊥底面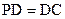 ,
,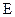 是
是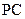 的中点,作
的中点,作 ⊥
⊥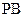 交
交 .
.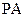 ∥平面
∥平面 ;
; .
.
 中,
中,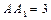 ,
,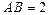 ,
,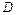 是
是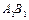 的中点,
的中点,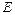 在线段
在线段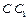 上且
上且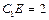 .(I)证明:
.(I)证明: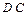
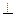 面
面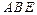 ;
;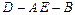 的大小.
的大小.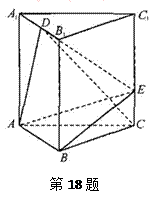
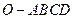 中,底面
中,底面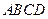 是边长为1的菱形,
是边长为1的菱形,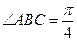 ,
,  ,
, 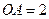 ,
, 为
为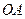 的中点,
的中点,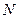 为
为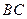 的中点.
的中点.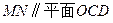 ;
;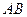 与
与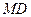 所成角的大小;
所成角的大小;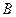 到平面
到平面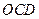 的距离.
的距离.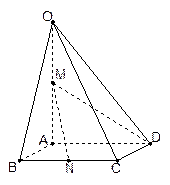
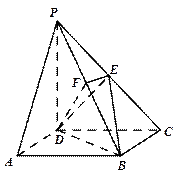
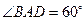 ,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.
,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.
 面PAD;
面PAD; 面DEF.
面DEF.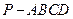 中,底面
中,底面 是边长为
是边长为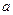 的正方形,
的正方形,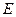 、
、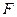 分别为
分别为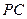 、
、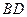 的中点,侧面
的中点,侧面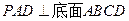 ,且
,且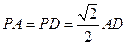 .
.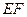 ∥平面
∥平面 ;(2)求三棱锥
;(2)求三棱锥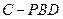 的体积.
的体积. 
 30°的纬线上,它们的经度差为
30°的纬线上,它们的经度差为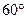 ,则A、B两点的球面距离为 ( )
,则A、B两点的球面距离为 ( )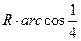 B.
B.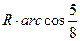 C.
C.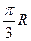 D.
D.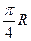
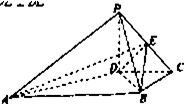
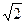 ,则球O的表面积为_______.
,则球O的表面积为_______.