题目内容
3.已知定义在R上的偶函数g(x)满足:当x≠0时,xg′(x)<0(其中g′(x)为函数g(x)的导函数);定义在R上的奇函数f(x)满足:f(x+2)=-f(x),在区间[0,1]上为单调递增函数,且函数y=f(x)在x=-5处的切线方程为y=-6.若关于x的不等式g[f(x)]≥g(a2-a+4)对x∈[6,10]恒成立,则a的取值范围是a≤-1或a≥2.分析 根据“xg′(x)<0”和导数与函数单调性的关系,判断出函数g(x)的单调性,再将“g[f(x)]≥g(a2-a+4)对x∈[6,10]恒成立”,转化为“|f(x)|≤|a2-a+4|对x∈[6,10]恒成立”,再由条件求出函数f(x)的周期、对称轴以及f(-5)的值,再得f(-1)、f(1)、f(3)的值,再由这些性质画出大致图象,右图象求出函数f(x)在[6,10]上的值域,从而求出最大值,列出关于a的不等式求解即可.
解答 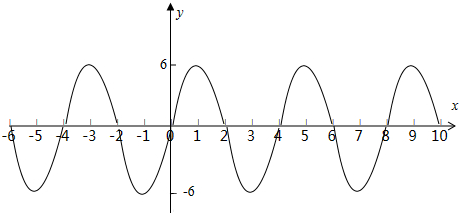 解:∵当x≠0时,xg′(x)<0,
解:∵当x≠0时,xg′(x)<0,
∴当x>0时,g′(x)<0,当x<0时,g′(x)>0,
即g(x)在(-∞,0)上递增,在(0,+∞)上递减,
∵不等式g[f(x)]≥g(a2-a+4)对x∈[6,10]恒成立,
∴|f(x)|≤|a2-a+4|对x∈[6,10]恒成立,
由f(x+2)=-f(x)得,f(x+4)=-f(x+2)=f(x),
则函数f(x)是以4为周期的周期函数,
又∵f(x)是R上的奇函数,
∴f(x+2)=-f(x)=f(-x),
则函数f(x)的对称轴是x=1,
∵在x=-5处的切线方程为y=-6,
∴f(-5)=-6,即f(-1)=f(3)=-6,f(1)=6,
再结合f(x)在区间[0,1]上为单调递增函数,且f(0)=0,画出大致图象:
由上图得,当x∈[6,10]时,f(x)∈[-6,6],
由|f(x)|≤|a2-a+4|对x∈[6,10]恒成立,
得6≤|a2-a+4|,
即a2-a+4≥6或a2-a+4≤-6,
化简得a2-a-2≥0或a2-a+10≤0,
解得a≤-1或a≥2,
故答案为:a≤-1或a≥2.
点评 本题主要考查有关函数性质的综合题,考查了导数与函数单调性的关系,函数的奇偶性与单调性关系、对称性、周期性等,考查了转化思想和数形结合思想,难度较大.


| A. | $\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | B. | -$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$ | C. | -$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | D. | 3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$ |
| A. | 5$\sqrt{2}$海里 | B. | 5 海里 | C. | 10$\sqrt{2}$海里 | D. | 10海里 |
| A. | [-3,-2] | B. | [-2,0] | C. | [-3,0] | D. | [-2,1] |
| A. | (-∞.-1) | B. | (1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-1,1) |