题目内容
11.已知△ABC的面积S=3,(1)若$\overrightarrow{AB}$•$\overrightarrow{AC}$∈[0,6],求∠A的取值范围;
(2)若∠A为钝角,a=4时,求:|$\frac{\overrightarrow{AB}}{{c}^{2}sin2B}$+$\frac{\overrightarrow{AC}}{{b}^{2}sin2C}$|的最小值.
分析 (1)根据三角形的面积公式可得到$|\overrightarrow{AB}||\overrightarrow{AC}|=\frac{6}{sinA}$,从而由$\overrightarrow{AB}•\overrightarrow{AC}∈[0,6]$即可得到$\frac{6cosA}{sinA}∈[0,6]$.容易说明A可以等于$\frac{π}{2}$,而$A≠\frac{π}{2}$时,便可得到tanA∈[1,+∞),从而得到A$∈[\frac{π}{4},\frac{π}{2})$,最后即可得出∠A的取值范围;
(2)作AD⊥BC,垂足为D,这样原式便可变成$|\frac{\overrightarrow{AB}}{2|\overrightarrow{AD}||\overrightarrow{BD}|}+\frac{\overrightarrow{AC}}{2|\overrightarrow{AD}||\overrightarrow{CD}|}|$,而$\overrightarrow{AB}=\overrightarrow{AD}+\overrightarrow{DB},\overrightarrow{AC}=\overrightarrow{AD}+\overrightarrow{DC}$,从而原式便等于$\frac{1}{2|\overrightarrow{AD}|}|\frac{\overrightarrow{AD}}{|\overrightarrow{BD}|}+\frac{\overrightarrow{AD}}{|\overrightarrow{CD}|}|=\frac{1}{2}|\frac{1}{|\overrightarrow{BD}|}+\frac{1}{|\overrightarrow{CD}|}|$,设$|\overrightarrow{BD}|=x$,从而$|\overrightarrow{CD}|=4-x$,x∈(0,4),从而原式=$\frac{2}{|-{x}^{2}+4x|}$,可以说明二次函数-x2+4x在x=2时取最大值,并此时|-x2+4x|取最大值,从而得出$|\frac{\overrightarrow{AB}}{{c}^{2}sin2B}+\frac{\overrightarrow{AC}}{{b}^{2}sin2C}|$的最小值.
解答  解:(1)由${S}_{△ABC}=\frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|sinA=3$得:$|\overrightarrow{AB}||\overrightarrow{AC}|=\frac{6}{sinA}$;
解:(1)由${S}_{△ABC}=\frac{1}{2}|\overrightarrow{AB}||\overrightarrow{AC}|sinA=3$得:$|\overrightarrow{AB}||\overrightarrow{AC}|=\frac{6}{sinA}$;
∴$\overrightarrow{AB}•\overrightarrow{AC}=|\overrightarrow{AB}||\overrightarrow{AC}|cosA=\frac{6cosA}{sinA}$∈[0,6];
(1)A=$\frac{π}{2}$时显然满足$\frac{6cosA}{sinA}$∈[0,6];
(2)A≠$\frac{π}{2}$时,可以得到$\frac{6}{\frac{sinA}{cosA}}∈(0,6]$;
∴$\frac{sinA}{cosA}=tanA∈[1,+∞)$;
∵0<A<π;
∴$A∈[\frac{π}{4},\frac{π}{2})$;
综上得∠A的取值范围为$[\frac{π}{4},\frac{π}{2}]$;
(2)如图,过A作AD|⊥BC,垂足为D,则:
$|\frac{\overrightarrow{AB}}{{c}^{2}sin2B}+\frac{\overrightarrow{AC}}{{b}^{2}sin2C}|$=|$\frac{\overrightarrow{AB}}{2csinB•ccosB}+\frac{\overrightarrow{AC}}{2bsinC•bcosC}$|=$|\frac{\overrightarrow{AB}}{2|\overrightarrow{AD}||\overrightarrow{BD}|}+\frac{\overrightarrow{AC}}{2|\overrightarrow{AD}||\overrightarrow{CD}|}|$
=$\frac{1}{2|\overrightarrow{AD}|}|\frac{\overrightarrow{AD}+\overrightarrow{DB}}{|\overrightarrow{BD}|}+\frac{\overrightarrow{AD}+\overrightarrow{DC}}{|\overrightarrow{CD}|}|$=$\frac{1}{2|\overrightarrow{AD}|}|\frac{\overrightarrow{AD}}{|\overrightarrow{BD}|}+\frac{\overrightarrow{AD}}{|\overrightarrow{CD}|}|$=$\frac{1}{2}|\frac{1}{|\overrightarrow{BD}|}+\frac{1}{|\overrightarrow{CD}|}|$;
设$|\overrightarrow{BD}|=x$,$|\overrightarrow{CD}|=4-x$,x∈(0,4);
原式=$\frac{1}{2}|\frac{1}{x}+\frac{1}{4-x}|=\frac{2}{|-{x}^{2}+4x|}$;
x∈(0,4)时,-x2+4x>0;
∴|-x2+4x|=-x2+4x;
二次函数-x2+4x当x=2时取最大值4;
即-x2+4x≤4,即|-x2+4x|≤4;
∴$\frac{2}{|-{x}^{2}+4x|}≥\frac{1}{2}$;
∴$|\frac{\overrightarrow{AB}}{{c}^{2}sin2B}+\frac{\overrightarrow{AC}}{{b}^{2}sin2C}|$的最小值为$\frac{1}{2}$.
点评 考查三角形面积公式,向量数量积的计算公式,求∠A范围时可结合正切函数图象,二倍角的正弦公式,正余弦函数的定义,向量加法的几何意义,单位向量的定义,以及二次函数的最值,含绝对值函数的最值的求法.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案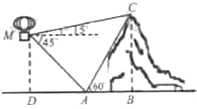 如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知∠BAC=60°,则山的高度BC为( )
如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知∠BAC=60°,则山的高度BC为( )| A. | 700 m | B. | 640 m | C. | 600 m | D. | 560 m |
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |