题目内容
15.已知不等式|x+a|+|x-3|≤|x-4|的解集包含[2,3],则a的取值范围为( )| A. | [-3,-2] | B. | [-2,0] | C. | [-3,0] | D. | [-2,1] |
分析 由题意可得,x=2和 x=3满足不等式|x+a|+|x-3|≤|x-4|,于是把x=2和 x=3分别代入不等式,求得a的范围,再取交集,即得所求.
解答 解:由题意可得,x=2和x=3满足不等式|x+a|+|x-3|≤|x-4|,
故有|2+a|+|2-3|≤|2-4|,即|2+a|≤1,-1≤2+a≤1,-3≤a≤-1.
|3+a|+|3-3|≤|3-4|,即|3+a|≤1,-1≤3+a≤1-4≤a≤-2.
综合可得-3≤a≤-2,
故选:A.
点评 本题主要考查绝对值不等式的解法,体现了等价转化的数学思想,属于基础题.

练习册系列答案
相关题目
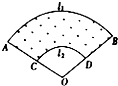 某小区设计的花坛形状如图中的阴影部分,已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,AC=BD=d,则花坛的面积为$\frac{1}{2}$d(l1+l2).
某小区设计的花坛形状如图中的阴影部分,已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,AC=BD=d,则花坛的面积为$\frac{1}{2}$d(l1+l2).