题目内容
13.函数f(x)(x∈R)满足f(1)=1,f′(1)=1,f′(x)<$\frac{1}{2}$,f(x2)<$\frac{1}{2}$x2+$\frac{1}{2}$.| A. | (-∞.-1) | B. | (1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-1,1) |
分析 根据条件构造F(x)=f(x)-$\frac{1}{2}$x-$\frac{1}{2}$,利用导数研究函数的单调性,然后将不等式进行转化,根据单调性建立关系,解之即可.
解答 解:令F(x)=f(x)-$\frac{1}{2}$x-$\frac{1}{2}$,
则F′(x)=f′(x)-$\frac{1}{2}$,
∵f′(x)<$\frac{1}{2}$,
∴F′(x)=f′(x)-$\frac{1}{2}$<0,
∴F(x)在R上单调递减
∵f(1)=1,∴F(1)=f(1)-$\frac{1}{2}$-$\frac{1}{2}$=1-1=0,
∴f(x)-$\frac{1}{2}$x-$\frac{1}{2}$<0等价为F(x)<0=F(1),
即x>1,
则不等式f(x)<$\frac{1}{2}$x+$\frac{1}{2}$的解为x>1,
由f(x2)<$\frac{1}{2}$x2+$\frac{1}{2}$.
可得x2>1,解得x>1或x<-1,
故不等式的解集为(-∞,-1)∪(1,+∞),
故选:C.
点评 本题考查不等式的求解,构造函数,利用导数研究函数的单调性是解决本题的关键.同时考查了转化思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知tanα=2,则$\frac{1+2sinαcosα}{{{{sin}^2}α-{{cos}^2}α}}$的值是( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -3 |
3.在一次考试中,5名同学数学、物理成绩如表所示:
(Ⅰ)根据表中数据,求物理分y对数学分x的回归方程.
(Ⅱ)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以X表示选中的同学中物理成绩高于90分的人数,求随机变量X的分布列及期望.(附:回归方程$\widehat{y}$=bx+a中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$)
| 学生 | A | B | C | D | E |
| 数学(x分) | 89 | 91 | 93 | 95 | 97 |
| 物理(y分) | 87 | 89 | 89 | 92 | 93 |
(Ⅱ)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以X表示选中的同学中物理成绩高于90分的人数,求随机变量X的分布列及期望.(附:回归方程$\widehat{y}$=bx+a中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$)
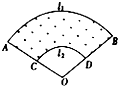 某小区设计的花坛形状如图中的阴影部分,已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,AC=BD=d,则花坛的面积为$\frac{1}{2}$d(l1+l2).
某小区设计的花坛形状如图中的阴影部分,已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,AC=BD=d,则花坛的面积为$\frac{1}{2}$d(l1+l2).