题目内容
13.f(x)=$\frac{{2{{cos}^4}x-2{{cos}^2}x+\frac{1}{2}}}{{2tan({\frac{π}{4}-x}){{cos}^2}({\frac{π}{4}-x})}}$(1)求$f({\frac{π}{12}})$;
(2)将f(x)的图象向右平移$\frac{π}{6}$得g(x)的图象,求g(x)的表达式,并问x为何值时g(x)最大.
分析 (1)利用三角函数中的恒等变换应用化简可得f(x)=$\frac{1}{2}$cos2x,代入x=$\frac{π}{12}$即可得解.
(2)由函数y=Asin(ωx+φ)的图象变换可得解析式g(x)=$\frac{1}{2}$cos(2x-$\frac{π}{3}$),由余弦函数的图象和性质即可得解.
解答 解:(1)∵f(x)=$\frac{{2{{cos}^4}x-2{{cos}^2}x+\frac{1}{2}}}{{2tan({\frac{π}{4}-x}){{cos}^2}({\frac{π}{4}-x})}}$=$\frac{(\sqrt{2}co{s}^{2}x-\frac{\sqrt{2}}{2})^{2}}{2sin(\frac{π}{4}-x)cos(\frac{π}{4}-x)}$=$\frac{\frac{1}{2}co{s}^{2}2x}{cos2x}$=$\frac{1}{2}$cos2x,
∴$f({\frac{π}{12}})$=$\frac{1}{2}$cos(2×$\frac{π}{12}$)=$\frac{1}{2}$cos$\frac{π}{6}$=$\frac{\sqrt{3}}{4}$.
(2)∵将f(x)的图象向右平移$\frac{π}{6}$得g(x)的图象,
∴g(x)=$\frac{1}{2}$cos2(x-$\frac{π}{6}$)=$\frac{1}{2}$cos(2x-$\frac{π}{3}$),
∴当2x-$\frac{π}{3}$=2kπ,k∈Z,即x=k$π+\frac{π}{6}$,k∈Z时,g(x)最大,最大值为:$\frac{1}{2}$.
点评 本题主要考查了三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换,余弦函数的图象和性质,属于基本知识的考查.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $(-∞,-\frac{1}{2})$ | B. | $(-5,-\frac{1}{2})$ | C. | $(-\frac{1}{2},5)$ | D. | $(-\frac{1}{2},+∞)$ |
| A. | (-2,1) | B. | (2,+∞) | C. | (-2,1)∪(2,+∞) | D. | (-∞,-2)∪(1,+∞) |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | 充分而不必要 | B. | 必要而不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
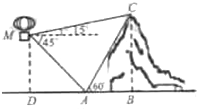 如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知∠BAC=60°,则山的高度BC为( )
如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知∠BAC=60°,则山的高度BC为( )| A. | 700 m | B. | 640 m | C. | 600 m | D. | 560 m |