题目内容
12.用坐标法证明:等腰三角形ABC底边上一点到两腰的距离和等于一腰上的高.分析 以BC所在的直线为x轴,BC的中垂线为y轴建立平面直角坐标系,设B(-a,0),C(a,0),A(0,b),求出|PD|,|PE|,点 C到 AB的距离|CF|.推出结果.
解答 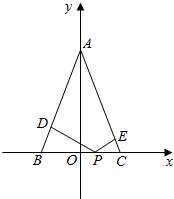 证明:在三角形中,AB=AC,P为底边BC上的一点,PD⊥AB与点D,PE⊥AC于点E,CF⊥AB于点F.
证明:在三角形中,AB=AC,P为底边BC上的一点,PD⊥AB与点D,PE⊥AC于点E,CF⊥AB于点F.
以BC所在的直线为x轴,BC的中垂线为y轴建立平面直角坐标系
设B(-a,0),C(a,0),A(0,b),则直线AB的方程是bx-ay+ab=0.
直线AC的方程是bx+ay+ab=0.设 P(x0,0),-a<x0<a
则点p到直线AB,AC的距离分别为
|PD|=$\frac{|{bx}_{0}-0+ab|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{{bx}_{0}+ab}{\sqrt{{a}^{2}+{b}^{2}}}$
|PE|=$\frac{|{bx}_{0}-ab|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{ab-{bx}_{0}}{\sqrt{{a}^{2}+{b}^{2}}}$
点 C到 AB的距离为
|CF|=$\frac{2ab}{\sqrt{{a}^{2}+{b}^{2}}}$,
∴|PD|+|PE|=|CF|
等腰三角形底边上一点到两腰的距离和等于一腰上的高.
点评 本题考查向量的几何中的应用,点到直线的距离个数的应用,考查计算能力.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
2.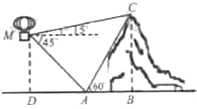 如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知∠BAC=60°,则山的高度BC为( )
如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知∠BAC=60°,则山的高度BC为( )
 如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知∠BAC=60°,则山的高度BC为( )
如图,在离地面高400m的热气球上,观测到山顶C处的仰角为15°,山脚A处的俯角为45°,已知∠BAC=60°,则山的高度BC为( )| A. | 700 m | B. | 640 m | C. | 600 m | D. | 560 m |