Question

【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等，A1在底面ABC内的射影为△ABC的中心，则AB1与底面ABC所成角的正弦值等于 ．

Answer 1

【答案】
【解析】解：由题意不妨令棱长为2，如图，A1在底面ABC内的射影为△ABC的中心，故DA= ，
由勾股定理得A1D= =
过B1作B1E⊥平面ABC，则∠B1AE为AB1与底面ABC所成角，且B1E= ，
如图作A1S⊥AB于中点S，∴A1S= ，
∴AB1= =2
∴AB1与底面ABC所成角的正弦值sin∠B1AE= = ．
所以答案是：

【考点精析】关于本题考查的空间角的异面直线所成的角，需要了解已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则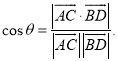才能得出正确答案．