题目内容
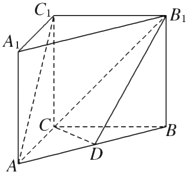
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60° 
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C= ![]() ,求三棱柱ABC﹣A1B1C1的体积.
,求三棱柱ABC﹣A1B1C1的体积.
【答案】
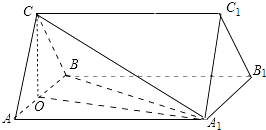
(1)证明:如图,
取AB的中点O,连结OC,OA1,A1B.
因为CA=CB,所以OC⊥AB.
由于AB=AA1, ![]() ,故△AA1B为等边三角形,
,故△AA1B为等边三角形,
所以OA1⊥AB.
因为OC∩OA1=O,所以AB⊥平面OA1C.
又A1C平面OA1C,故AB⊥A1C;
(2)解:由题设知△ABC与△AA1B都是边长为2的等边三角形,
所以 ![]() .
.
又 ![]() ,则
,则 ![]() ,故OA1⊥OC.
,故OA1⊥OC.
因为OC∩AB=O,所以OA1⊥平面ABC,OA1为三棱柱ABC﹣A1B1C1的高.
又△ABC的面积 ![]() ,故三棱柱ABC﹣A1B1C1的体积
,故三棱柱ABC﹣A1B1C1的体积 ![]() .
.
【解析】(1)由题目给出的边的关系,可想到去AB中点O,连结OC,OA1 , 可通过证明AB⊥平面OA1C得要证的结论;(2)在三角形OCA1中,由勾股定理得到OA1⊥OC,再根据OA1⊥AB,得到OA1为三棱柱ABC﹣A1B1C1的高,利用已知给出的边的长度,直接利用棱柱体积公式求体积.
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点,需要掌握垂直于同一个平面的两条直线平行才能正确解答此题.

练习册系列答案
相关题目