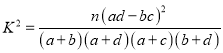Question

【题目】已知函数f（x）=x2+bx+c（b，c∈R），并设 ，
（1）若F（x）图像在x=0处的切线方程为x﹣y=0，求b、c的值；
（2）若函数F（x）是（﹣∞，+∞）上单调递减，则 ①当x≥0时，试判断f（x）与（x+c）2的大小关系，并证明之；
②对满足题设条件的任意b、c，不等式f（c）﹣Mc2≤f（b）﹣Mb2恒成立，求M的取值范围．

Answer 1

【答案】
（1）解：因为 ，所以 ，

又因为F（x）图像在x=0处的切线方程为x﹣y=0，

所以 ，即 ，解得 b=1，c=0

（2）解：①因为F（x）是（﹣∞，+∞）上的单调递减函数，所以F′（x）≤0恒成立，

即﹣x2+（2﹣b）x+（b﹣c）≤0对任意的x∈R恒成立，

所以△=（2﹣b）2+4（b﹣c）≤0，所以 ，即c＞b且c≥1，

令g（x）=f（x）﹣（x+c）2=（b﹣2c）x﹣c（c﹣1），由b﹣2c＜0，知g（x）是减函数，

故g（x）在[0，+∞）内取得最小值g（0），又g（0）=﹣c（c﹣1）≤0，

所以x≥0时，g（x）≤g（0）≤0，即f（x）≤（x+c）2．

②由①知，c≥|b|≥0，当|b|=c时，b=c或b=﹣c，

因为b2+4﹣4c≤0，即c2+4﹣4c≤0，解得c=2，b=2或b=﹣2，所以f（x）=x2±2x+2，

而f（c）﹣f（b）=c2+bc+c﹣b2﹣b2﹣c=c2+bc﹣2b2=（c+2b）（c﹣b），

所以f（c）﹣f（b）=﹣8或0，

不等式f（c）﹣Mc2≤f（b）﹣Mb2等价于f（c）﹣f（b）≤M（c2﹣b2），

变为﹣8≤M0或0≤M0恒成立，M∈R，

当|b|≠c时，c＞|b|，即c2﹣b2＞0，所以不等式f（c）﹣Mc2≤f（b）﹣Mb2恒成立等价于 恒成立，等价于 ，

而 ，

因为c＞|b|， ，所以 ，所以 ，所以 ，

所以 ，所以

【解析】（1）欲求b，c的值，根据所给的切线方程，只须求出切线斜率即可，故先利用导数求出在x=0处的导函数值，再结合导数的几何意义即可求出切线的斜率进而得切线方程，最后与所给的方程比较即得b，c的值；（2）根据函数F（x）是（﹣∞，+∞）上单调递减，得到F′（x）≤0恒成立，从而得到c＞b且c≥1，①令g（x）=f（x）﹣（x+c）2=（b﹣2c）x﹣c（c﹣1），从而得到结果；②不等式f（c）﹣Mc2≤f（b）﹣Mb2恒成立等价于f（c）﹣f（b）≤M（c2﹣b2）恒成立，分离参数可得 恒成立，转化为求 的最大值即可．
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案，需要熟知一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．