题目内容
【题目】已知一个分段函数可利用函数 ![]() 来表示,例如要表示一个分段函数
来表示,例如要表示一个分段函数 ![]() ,可将函数g(x)表示为g(x)=xS(x﹣2)+(﹣x)S(2﹣x).现有一个函数f(x)=(﹣x2+4x﹣3)S(x﹣1)+(x2﹣1)S(1﹣x).
,可将函数g(x)表示为g(x)=xS(x﹣2)+(﹣x)S(2﹣x).现有一个函数f(x)=(﹣x2+4x﹣3)S(x﹣1)+(x2﹣1)S(1﹣x).
(1)求函数f(x)在区间[0,4]上的最大值与最小值;
(2)若关于x的不等式f(x)≤kx对任意x∈[0,+∞)都成立,求实数k的取值范围.
【答案】
(1)解:由题意可知 ![]() ,
,
当1≤x≤4时,f(x)=﹣(x﹣2)2+1,则f(x)在[1,2]上递增,在[2,4]上递减;
当0≤x<1时,f(x)=x2﹣1,则f(x)在[0,1)上递增,
而f(0)=﹣1,f(2)=1,f(4)=﹣3,所以f(x)max=f(2)=1,f(x)min=f(4)=﹣3
(2)解:由图可知,
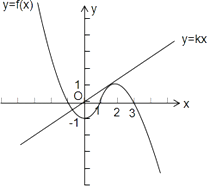
当直线y=kx与抛物线y=﹣x2+4x﹣3只有一个交点时,令kx=﹣x2+4x﹣3,即x2+(k﹣4)x+3=0,由△=0,得(k﹣4)2﹣12=0,得k=4±2 ![]() ,
,
结合图像,可知当k≥4﹣2 ![]() 时,关于x的不等式f(x)≤kx对任意x∈[0,+∞)都成立
时,关于x的不等式f(x)≤kx对任意x∈[0,+∞)都成立
【解析】(1)由题意可知 ![]() ,利用二次函数的单调性可求得函数f(x)在区间[0,4]上的最大值与最小值;(2)在同一坐标系中作出y=f(x)与y=kx的图像,令kx=﹣x2+4x﹣3,即x2+(k﹣4)x+3=0,由△=0可求得k的值,结合图像可求得,对任意x∈[0,+∞)都成立时,实数k的取值范围.
,利用二次函数的单调性可求得函数f(x)在区间[0,4]上的最大值与最小值;(2)在同一坐标系中作出y=f(x)与y=kx的图像,令kx=﹣x2+4x﹣3,即x2+(k﹣4)x+3=0,由△=0可求得k的值,结合图像可求得,对任意x∈[0,+∞)都成立时,实数k的取值范围.
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
