题目内容
【题目】如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米) 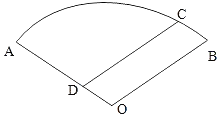
【答案】解:法一:设该扇形的半径为r米,连接CO. 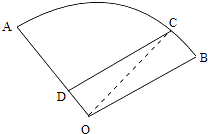
由题意,得CD=500(米),DA=300(米),∠CDO=60°
在△CDO中,CD2+OD2﹣2CDODcos60°=OC2
即, ![]()
解得 ![]() (米)
(米)
答:该扇形的半径OA的长约为445米.
法二:连接AC,作OH⊥AC,交AC于H,
由题意,得CD=500(米),AD=300(米),∠CDA=120°
在△CDO中,AC2=CD2+AD2﹣2CDADcos120°= ![]() .
.
∴AC=700(米).![]() .
.
在直角△HAO中,AH=350(米), ![]() ,
,
∴ ![]() (米).
(米).
答:该扇形的半径OA的长约为445米.
【解析】连接OC,由CD∥OB知∠CDO=60°,可由余弦定理得到OC的长度.

【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销![]() 天,两个厂家提供的返利,方案如下:甲厂家每天固定返利
天,两个厂家提供的返利,方案如下:甲厂家每天固定返利![]() 元,且每卖出一件产品厂家再返利
元,且每卖出一件产品厂家再返利![]() 元,乙厂家无固定返利,卖出
元,乙厂家无固定返利,卖出![]() 件以内(含
件以内(含![]() 件)的产品,每件产品厂家返利
件)的产品,每件产品厂家返利![]() 元,超出
元,超出![]() 件的部分每件返利
件的部分每件返利![]() 元,分别记录其
元,分别记录其![]() 天内的销售件数,得到如下频数表:
天内的销售件数,得到如下频数表:
甲厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
乙厂家销售件数频数表:
销售件数 |
|
|
|
|
|
天数 |
|
|
|
|
|
(1) 现从甲厂家试销的![]() 天中抽取两天,求一天销售量大于
天中抽取两天,求一天销售量大于![]() 而另一天销售量小于
而另一天销售量小于![]() 的概率;
的概率;
(2)若将频率视作概率,回答以下问题:
①记乙厂家的日返利为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.