题目内容
【题目】已知函数y=f(x)在定义域(﹣ ![]() ,3)内可导,其图像如图所示.记y=f(x)的导函数为y=f′(x),则不等式
,3)内可导,其图像如图所示.记y=f(x)的导函数为y=f′(x),则不等式 ![]() ≤0的解集为 .
≤0的解集为 . 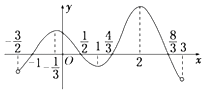
【答案】[2,3]∪[﹣ ![]() ,﹣
,﹣ ![]() ]
]
【解析】解:不等式 ![]() ≤0,等价于
≤0,等价于 ![]() ①,或
①,或 ![]() ②.
②.
由y=f(x)图像可知f(x)在[﹣ ![]() ,1]、[2,3]内递减,f′(x)≤0;
,1]、[2,3]内递减,f′(x)≤0;
f(x)在[﹣ ![]() ,﹣
,﹣ ![]() ]、[1,2]内递增,f′(x)≥0.
]、[1,2]内递增,f′(x)≥0.
故由①可得x∈[2,3],由②可得x∈[﹣ ![]() ,﹣
,﹣ ![]() ].
].
综上可得,不等式 ![]() ≤0的解集为[2,3]∪[﹣
≤0的解集为[2,3]∪[﹣ ![]() ,﹣
,﹣ ![]() ],
],
所以答案是:[2,3]∪[﹣ ![]() ,﹣
,﹣ ![]() ].
].
【考点精析】认真审题,首先需要了解函数单调性的性质(函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集),还要掌握导数的几何意义(通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.

练习册系列答案
相关题目

