题目内容
7.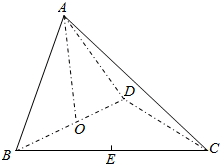 如图,在三棱锥A-BCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=$\sqrt{2}$.
如图,在三棱锥A-BCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=$\sqrt{2}$.(1)求证:AO⊥平面BCD;
(2)求三棱锥A-BCD体积.
分析 (1)连接OC,证明AO⊥BD,CO⊥BD,AO⊥OC,利用直线与平面垂直的判定定理证明AO⊥平面BCD.
(2)求出三棱锥A-BCD的高,底面面积,即可求解三棱锥A-BCD体积.
解答 (1)证明:连接OC,∵BO=DO,AB=AD∴AO⊥BD-----------(1分)
∵BO=DO,BC=CD∴CO⊥BD-------------(2分)
在△AOC中,由已知可得:$AO=1,CO=\sqrt{3}$,而AC=2,
∴AO2+CO2=AC2∴∠AOC=90°,即AO⊥OC-------(4分)
∵BD∩OC=O,
∴AO⊥平面BCD----------(5分).
(2)解:由(1)可知三棱锥A-BCD的高为AO=1,底面面积为:S=$\frac{\sqrt{3}}{4}×{2}^{2}$=$\sqrt{3}$.
三棱锥A-BCD体积为:$\frac{1}{3}×\sqrt{3}×1=\frac{\sqrt{3}}{3}$.
点评 本题考查三棱锥的体积的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
17.与角-420°终边相同的角是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
 把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有k个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(63,62).
把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有k个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(63,62).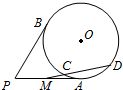 如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=8,MC=2,则CD=6.
如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=8,MC=2,则CD=6.