题目内容
2．观察数列$\sqrt{3}$，3，$\sqrt{15}$，$\sqrt{21}$，3$\sqrt{3}$，…，写出数列的一个通项公式an=$\sqrt{6n-3}$．分析 根据数列项的规律求出数列的通项公式即可．
解答 解：数列等价为$\sqrt{3}$，$\sqrt{9}$，$\sqrt{15}$，$\sqrt{21}$，$\sqrt{27}$，…，
则对应的通项公式为an=$\sqrt{6n-3}$，
故答案为：${a_n}=\sqrt{6n-3}$
点评 本题主要考查数列的概念和简单表示，求出数列的规律是解决本题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
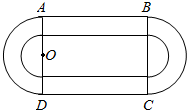某学校要建造一个面积为10000平方米的运动场．如图，运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成．跑道是一条宽8米的塑胶跑道，运动场除跑道外，其他地方均铺设草皮．已知塑胶跑道每平方米造价为150元，草皮每平方米造价为30元．
17．
如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图，中间的数字表示得分的十位数，据图可知（ ）
如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图，中间的数字表示得分的十位数，据图可知（ ）| A． | 甲运动员的最低得分为0分 | |
| B． | 乙运动员得分的中位数是29 | |
| C． | 甲运动员得分的众数为44 | |
| D． | 乙运动员得分的平均值在区间（11，19）内 |
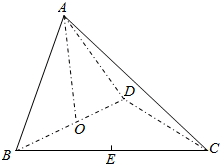如图，在三棱锥A-BCD中，O，E分别是BD，BC的中点，CA=CB=CD=BD=2，AB=AD=$\sqrt{2}$．