题目内容
19.若关于x的方程x2-ax+1-a=0在区间[2,+∞)上有解,则a的取值范围是[$\frac{5}{3}$,+∞).分析 由x2-ax+1-a=0分离参变量得a=$\frac{{x}^{2}+1}{x+1}$,求函数的值域即可.
解答 解:x2-ax+1-a=0在区间[2,+∞) 上有解,
即a=$\frac{{x}^{2}+1}{x+1}$在区间[2,+∞)上有解,
令y=$\frac{{x}^{2}+1}{x+1}$则y′=$\frac{{x}^{2}+2x-1}{{(x+1)}^{2}}$>0对x∈[2,+∞) 恒成立,
∴y=$\frac{{x}^{2}+1}{x+1}$在[2,+∞) 上是增函数,
故y≥y(2)=$\frac{5}{3}$,故函数的值域为:[$\frac{5}{3}$,+∞),
故a的取值范围是:[$\frac{5}{3}$,+∞),
故答案为:[$\frac{5}{3}$,+∞).
点评 本题考查了函数的值域问题,分离参变量得a=$\frac{{x}^{2}+1}{x+1}$是解题的关键,属于中档题.

练习册系列答案
相关题目
9.函数y=sin2x+cos2x的值域是( )
| A. | [-1,1] | B. | [-2,2] | C. | [-1,$\sqrt{2}$] | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
4.若函数y=f(x-1)的图象过点(2,3),则( )
| A. | f(2)=3 | B. | f(3)=2 | C. | f(1)=3 | D. | f(3)=1 |
8.已知x、y的取值如表所示:
若从散点图分析,y与x线性相关,且线性回归直线方程为$\widehat{y}$=0.95x+$\widehat{a}$,则$\widehat{a}$的值等于2.6.
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
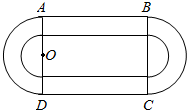 某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.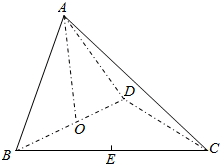 如图,在三棱锥A-BCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=$\sqrt{2}$.
如图,在三棱锥A-BCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=$\sqrt{2}$.