题目内容
16.函数f(x)=sinx+cosx的单调增区间为$[-\frac{3}{4}π+2kπ,\frac{π}{4}+2kπ]k∈Z$;已知$cos(α+\frac{π}{12})=\frac{3}{5}$,且$α∈(0,\frac{π}{2})$,则$f(2α+\frac{π}{12})$=$\frac{{24\sqrt{6}-7\sqrt{2}}}{50}$.分析 化简可得f(x)=$\sqrt{2}$sin(x+$\frac{π}{4}$),解不等式2kπ-$\frac{π}{2}$≤x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$可得;由题意可得sin(α+$\frac{π}{12}$),进而由二倍角公式可得cos(2α+$\frac{π}{6}$)和sin(2α+$\frac{π}{6}$),而$f(2α+\frac{π}{12})$=$\sqrt{2}$sin(2α+$\frac{π}{6}$+$\frac{π}{6}$)=$\sqrt{2}$×$\frac{\sqrt{3}}{2}$sin(2α+$\frac{π}{6}$)+$\sqrt{2}$×$\frac{1}{2}$cos(2α+$\frac{π}{6}$),代值计算可得.
解答 解:化简可得f(x)=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),
由2kπ-$\frac{π}{2}$≤x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$可得2kπ-$\frac{3π}{4}$≤x≤2kπ+$\frac{π}{4}$,
∴函数的单调递增区间为:$[-\frac{3}{4}π+2kπ,\frac{π}{4}+2kπ]k∈Z$;
∵$cos(α+\frac{π}{12})=\frac{3}{5}$,且$α∈(0,\frac{π}{2})$,
∴sin(α+$\frac{π}{12}$)=$\frac{4}{5}$,
∴cos(2α+$\frac{π}{6}$)=2cos2(α+$\frac{π}{12}$)-1=-$\frac{7}{25}$,
∴sin(2α+$\frac{π}{6}$)=2sin(α+$\frac{π}{12}$)cos(α+$\frac{π}{12}$)=$\frac{24}{25}$
∴$f(2α+\frac{π}{12})$=$\sqrt{2}$sin(2α+$\frac{π}{12}$+$\frac{π}{4}$)
=$\sqrt{2}$sin(2α+$\frac{π}{3}$)=$\sqrt{2}$sin(2α+$\frac{π}{6}$+$\frac{π}{6}$)
=$\sqrt{2}$×$\frac{\sqrt{3}}{2}$sin(2α+$\frac{π}{6}$)+$\sqrt{2}$×$\frac{1}{2}$cos(2α+$\frac{π}{6}$)
=$\frac{\sqrt{6}}{2}$×$\frac{24}{25}$+$\frac{\sqrt{2}}{2}$×(-$\frac{7}{25}$)=$\frac{{24\sqrt{6}-7\sqrt{2}}}{50}$
故答案为:$[-\frac{3}{4}π+2kπ,\frac{π}{4}+2kπ]k∈Z$;$\frac{{24\sqrt{6}-7\sqrt{2}}}{50}$
点评 本题考查两角和与差的三角函数,涉及三角函数的单调性,属中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | f(2)=3 | B. | f(3)=2 | C. | f(1)=3 | D. | f(3)=1 |
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 6 |
| A. | 假设a,b,c中只有一个为0 | B. | 假设a,b,c都不为0 | ||
| C. | 假设a,b,c都为0 | D. | 假设a,b,c不都为0 |
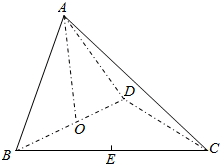 如图,在三棱锥A-BCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=$\sqrt{2}$.
如图,在三棱锥A-BCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=$\sqrt{2}$.