题目内容
17．计算：C${\;}_{4}^{3}$+C${\;}_{5}^{3}$+…+C${\;}_{10}^{3}$=329．分析 利用组合数公式${C}_{n}^{m+1}$+${C}_{n}^{m}$=${C}_{n+1}^{m+1}$进行化简即可．
解答 解：C${\;}_{4}^{3}$+C${\;}_{5}^{3}$+…+C${\;}_{10}^{3}$=（${C}_{4}^{4}$+${C}_{4}^{3}$）+${C}_{5}^{3}$+…+${C}_{10}^{3}$-1
=${C}_{5}^{4}$+${C}_{5}^{3}$+…+${C}_{10}^{3}$-1
=${C}_{6}^{4}$+…+${C}_{10}^{3}$-1
=${C}_{10}^{4}$+${C}_{10}^{3}$-1
=${C}_{11}^{4}$-1
=329．
故答案为：329．
点评 本题考查了组合数公式的应用问题，也考查了公式灵活应用的问题，是基础题目．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
8．已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1，F2，过右焦点F2作x轴的垂线，交椭圆于A，B两点．若等边△ABF1的周长为$4\sqrt{3}$，则椭圆的方程为（ ）
| A． | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | B． | $\frac{x^2}{3}+\frac{y^2}{6}=1$ | C． | $\frac{x^2}{2}+\frac{y^2}{3}=1$ | D． | $\frac{x^2}{9}+\frac{y^2}{4}=1$ |
9．函数y=sin2x+cos2x的值域是（ ）
| A． | [-1，1] | B． | [-2，2] | C． | [-1，$\sqrt{2}$] | D． | [-$\sqrt{2}$，$\sqrt{2}$] |
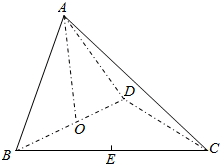如图，在三棱锥A-BCD中，O，E分别是BD，BC的中点，CA=CB=CD=BD=2，AB=AD=$\sqrt{2}$．