题目内容
6.若函数f(x)=sin($\frac{π}{4}$+x)sin($\frac{π}{4}$-x),则f(x)在[-$\frac{π}{8}$,$\frac{π}{8}$]上的最大值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 与积化和差公式对已知函数进行转化,然后根据余弦函数的最大值,求出此函数在定义域内的最大值.
解答 解:f(x)=sin($\frac{π}{4}$+x)sin($\frac{π}{4}$-x)=$\frac{1}{2}$cos2x-$\frac{1}{2}$sin2x=$\frac{1}{2}$cos2x.
∵x∈[-$\frac{π}{8}$,$\frac{π}{8}$],
∴2x∈[-$\frac{π}{4}$,$\frac{π}{4}$],
∴$\frac{1}{2}$cos2x的最大值是$\frac{1}{2}$.
故选:C.
点评 本题考查了三角函数的最值.根据已知函数得到f(x)=$\frac{1}{2}$cos2x是解题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
15.已知集合A={y|y=x2+2x-3},$B=\left\{{\left.y\right|y=x+\frac{1}{x},x>0}\right\}$,则有( )
| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=φ |
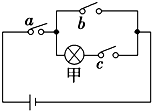 如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$.
如图所示的电路有a,b,c三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且是相互独立的,则灯泡甲亮的概率为$\frac{1}{8}$.