已知集合A={y|y=x2+2x-3}.$B=\left\{{\left.y\right|y=x+\frac{1}{x}.x＞0}\right\}$.则有( )A．A⊆BB．B⊆AC．A=BD．A∩B=φ 题目和参考答案——青夏教育精英家教网—

题目内容

15．已知集合A={y|y=x²+2x-3}，$B=\left\{{\left.y\right|y=x+\frac{1}{x}，x＞0}\right\}$，则有（　　）

A．

A⊆B

B．

B⊆A

C．

A=B

D．

A∩B=φ

分析利用二次函数最值的求法得到集合A，利用基本不等式的解法求得集合B，然后来求集合A、B的关系．

解答解：∵y=x²+2x-3=（x+1）²-4，
∴y≥-4．
则A={y|y≥-4}．
∵x＞0，
∴x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2（当x=$\frac{1}{x}$，即x=1时取“=”），
∴B={y|y≥2}，
∴B⊆A．
故选：B．

点评本题考查子集与真子集，求解本题，关键是将两个集合进行化简，由子集的定义得出两个集合之间的关系，再对比选项得出正确选项．

练习册系列答案

6．若函数f（x）=sin（$\frac{π}{4}$+x）sin（$\frac{π}{4}$-x），则f（x）在[-$\frac{π}{8}$，$\frac{π}{8}$]上的最大值为（　　）

3．（1-x）¹⁰的展开式中x³的系数为（　　）

10．已知实数x，y，z满足x+y+z=1，则x²+y²+z²的最小值为$\frac{1}{3}$．

20．如果对任意一个三角形，只要它的三边a，b，c都在函数f（x）的定义域内，就有f（a），f（b），f（c）也是某个三角形的三边长，则称f（x）为“和美型函数”．现有下列函数：①f（x）=$\sqrt{x}$； ②g（x）=sinx，x∈（0，π）； ③φ（x）=2^x；④h（x）=lnx，x∈[2，+∞）．其中是“和美型函数”的函数序号为①④．（写出所有正确的序号）

7．

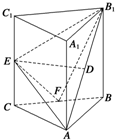三棱柱ABC-A₁B₁C₁中，侧棱AA₁⊥平面ABC，△ABC为等腰直角三角形，∠BAC=90°且AB=AA₁，D，E，F分别是B₁A，CC₁，BC的中点．
（1）求证：DE∥平面ABC；
（2）求证：B₁F⊥平面AEF．

4．已知集合A={0，1，2}，集合B={-1，0，1}，则集合A∩B=（　　）

5．设a=log_π3，b=2^0.3，c=log₂$\frac{1}{3}$，则a，b，c的大小关系为（　　）

试题分类