题目内容
16.已知椭圆的标准方程为:$\frac{x^2}{4}+\frac{y^2}{3}=1$,一个过点P(2,-3)的双曲线的长轴的端点为椭圆的焦点,求双曲线的标准方程.分析 先求出椭圆长轴端点,可得双曲线的焦点为F1(-2,0),F2(2,0),焦点在x轴上且c=2,再利用双曲线的定义,求出a,可得b,即可求双曲线的标准方程.
解答 解:由椭圆的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$,知:椭圆的长轴端点为(-2,0)和(2,0),
所以,双曲线的焦点为F1(-2,0),F2(2,0),焦点在x轴上且c=2.
由双曲线的定义知,2a=|$\sqrt{(-2-2)^{2}+(0+3)^{2}}$-$\sqrt{(2-2)^{2}+(0+3)^{2}}$|=5-3=2.
所以a=1,
所以b=$\sqrt{3}$,
所以双曲线的标准方程为${x}^{2}-\frac{{y}^{2}}{3}=1$.
点评 本题考查椭圆的方程与性质,考查双曲线的定义与方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
6.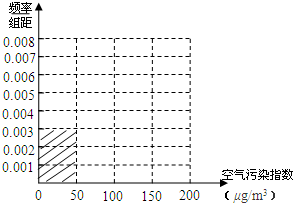 当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.某日某省x个监测点数据统计如下:
当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.某日某省x个监测点数据统计如下:
(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
 当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.某日某省x个监测点数据统计如下:
当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.某日某省x个监测点数据统计如下:| 空气污染指数(单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
8.已知正实数a,b满足:a+b=2,记$\frac{1}{a}+\frac{1}{b}$的最小值m.设函数$f(x)=|x-t|+|x+\frac{1}{t}|(t≠0)$,若存在实数x,使得f(x)=m,则x的取值范围为( )
| A. | [-1,1] | B. | [-2,2] | C. | [-1,0] | D. | [0,1] |
5.已知f(x)=$\frac{1}{2}$x2-alnx在区间(0,2)上不单调,实数a的取值范围是( )
| A. | (-2,0)∪(0,2) | B. | (-4,0)∪(0,4) | C. | (0,2) | D. | (0,4) |
6.若函数f(x)=sin($\frac{π}{4}$+x)sin($\frac{π}{4}$-x),则f(x)在[-$\frac{π}{8}$,$\frac{π}{8}$]上的最大值为( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |