题目内容
13.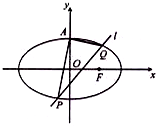 已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的上顶点为A,直线l:y=kx+m交椭圆P,Q两点,设直线AP,AQ的斜率分别为k1,k2.
已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的上顶点为A,直线l:y=kx+m交椭圆P,Q两点,设直线AP,AQ的斜率分别为k1,k2.(1)若m=0,时求k1•k2的值;
(2)若k1•k2=-1时,证明直线l:y=kx+m过定点.
分析 (1)若m=0时,直线l:y=kx代入椭圆方程得到x2+2k2x2=4,求出P,Q的坐标,即可求k1•k2的值;
(2)直线l:y=kx+m代入椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,k1•k2=-1时,$\frac{{y}_{1}-\sqrt{2}}{{x}_{1}}•\frac{{y}_{2}-\sqrt{2}}{{x}_{2}}=-1$,代入化简可得3m2-2$\sqrt{2}$m-2=0,求出m,即可证明直线l:y=kx+m过定点.
解答 解:(1)若m=0时,直线l:y=kx代入椭圆方程得到x2+2k2x2=4,
∴P(-$\frac{2}{\sqrt{1+2{k}^{2}}}$,-$\frac{2k}{\sqrt{1+2{k}^{2}}}$),Q($\frac{2}{\sqrt{1+2{k}^{2}}}$,$\frac{2k}{\sqrt{1+2{k}^{2}}}$),
∴k1=$\frac{2k+\sqrt{2}•\sqrt{1+2{k}^{2}}}{2}$,k2=$\frac{2k-\sqrt{2}•\sqrt{1+2{k}^{2}}}{2}$,
∴k1•k2=$\frac{2k+\sqrt{2}•\sqrt{1+2{k}^{2}}}{2}$•$\frac{2k-\sqrt{2}•\sqrt{1+2{k}^{2}}}{2}$=-$\frac{1}{2}$;
(2)设P(x1,y1),Q(x2,y2),直线l:y=kx+m代入椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,
整理得(1+2k2)x2+4kmx+2m2-4=0,
∴x1+x2=-$\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-4}{1+2{k}^{2}}$,
∵k1•k2=-1,
∴$\frac{{y}_{1}-\sqrt{2}}{{x}_{1}}•\frac{{y}_{2}-\sqrt{2}}{{x}_{2}}=-1$,
∴(kx1+m)(kx2+m)-$\sqrt{2}$(kx1+m+kx2+m)+x1x2+2=0,
代入化简可得3m2-2$\sqrt{2}$m-2=0,
∴m=$\sqrt{2}$(舍)或m=-$\frac{\sqrt{2}}{3}$,
∴直线l:y=kx+m过定点(0,-$\frac{\sqrt{2}}{3}$).
点评 本题考查椭圆方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

| A. | an=3•2n-1-2 | B. | an=3•2n-2 | C. | an=3•4n-1-2 | D. | an=3•2n+1-2 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$一l |
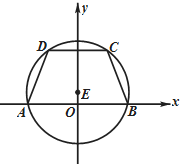 如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.
如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.