题目内容
5．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点为F，若F关于直线$\sqrt{3}$x+y=0的对称点A是椭圆C上的点，则椭圆C的离心率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}-1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\sqrt{3}$一l |
分析 求出F（-c，0）关于直线$\sqrt{3}$x+y=0的对称点A的坐标，代入椭圆方程可得离心率．
解答 解：设F（-c，0）关于直线$\sqrt{3}$x+y=0的对称点A（m，n），则$\left\{\begin{array}{l}{\frac{n}{m+c}•（-\sqrt{3}）=-1}\\{\sqrt{3}•\frac{m-c}{2}+\frac{n}{2}=0}\end{array}\right.$，
∴m=$\frac{c}{2}$，n=$\frac{\sqrt{3}}{2}$c，
代入椭圆方程可得$\frac{\frac{{c}^{2}}{4}}{{a}^{2}}+\frac{\frac{3}{4}{c}^{2}}{{b}^{2}}=1$，
化简可得e4-8e2+4=0，
∴e=$\sqrt{3}$-1，
故选：D．
点评 本题考查椭圆的方程简单性质的应用，考查对称知识以及计算能力．
练习册系列答案
相关题目
16．设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为e=$\frac{1}{2}$，右焦点为F（c，0），方程ax2+bx-c=0的两个实根分别为x1和x2，则点P（x1，x2）（ ）
| A． | 必在圆x2+y2=2上 | B． | 必在圆x2+y2=2外 | ||
| C． | 必在圆x2+y2=2内 | D． | 以上三种情形都有可能 |
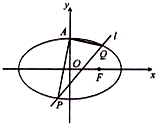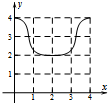
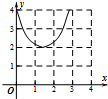
已知椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的上顶点为A，直线l：y=kx+m交椭圆P，Q两点，设直线AP，AQ的斜率分别为k1，k2．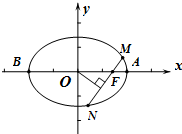
如图：已知方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的椭圆，A，B为顶点，过右焦点的弦MN的长度为y，中心O到弦MN的距离为d，点M从右顶点A开始按逆时针方向在椭圆上移动到B停止，当0°≤∠MFA≤90°时，记x=d，当90°＜∠MFA≤180°，记x=2$\sqrt{2}$-d，函数y=f（x）图象是（ ）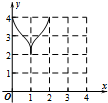
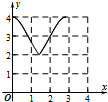
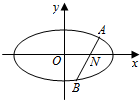如图，设过点N（1，0）的动直线l交椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）于A，B两点，且|AB|的最大值为4，椭圆C的离心率e=$\frac{\sqrt{3}}{2}$．